设f: 是集合A到集合B的映射,如果B={1,2},则
是集合A到集合B的映射,如果B={1,2},则 为 ( )
为 ( )
A. | B.{1} | C. 或{2} 或{2} | D. 或{1} 或{1} |
已知复数 ,在映射下
,在映射下 的象是
的象是 ,则
,则 的原象为
的原象为
A. | B. | C. | D.2 |
设f、g都是由A到A的映射,其对应法则如下表:
映射f的对应法则 映射g的对应法则
| 原象 | 1 | 2 | 3 | 4 |
| 象 | 3 | 4 | 2 | 1 |
| 原象 | 1 | 2 | 3 | 4 |
| 象 | 4 | 3 | 1 | 2 |
| A.g [f (1)] | B.g[f (2)] | C.g [f (3)] | D.g[f (4)] |
从集合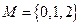 到集合
到集合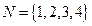 的不同映射的个数是( )
的不同映射的个数是( )
| A.81个 | B.64个 | C.24个 | D.12 个 个 |
我们为了探究函数  的部分性质,先列表如下:
的部分性质,先列表如下:
| x | … | 0.5 | 1 | 1.5 | 1.7 | 1.9 | 2 | 2.1 | 2.2 | 2.3 | 3 | 4 | 5 | 7 | … |
| y | … | 8.5 | 5 | 4.17 | 4.05 | 4.005 | 4 | 4.005 | 4.02 | 4.04 | 4.3 | 5 | 5.8 | 7.57 | … |
请你观察表中y值随x值变化的特点,完成以下的问题.
首先比较容易的看出来:此函数在区间(0,2)上是递减的;
(1)函数
 在区间 上递增.
在区间 上递增.当
 时,
时, .
.(2)请你根据上面性质作出此函数的大概图像;
 (3)证明:此函数在区间上(0,2)是递减的.
(3)证明:此函数在区间上(0,2)是递减的. 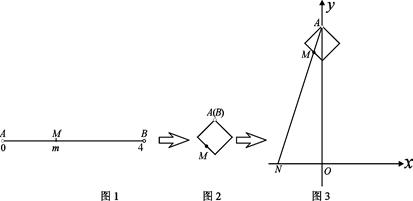
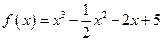 .
. 的单调区间;
的单调区间;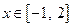 时
时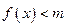 恒成立,求
恒成立,求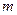 的取值范围。
的取值范围。 ,且对任意
,且对任意 ,有
,有 .
. ;
; 在区间(0,1)上为单调函数,求实
在区间(0,1)上为单调函数,求实 数
数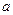 的取值范围.
的取值范围. 的零点个数?(提示
的零点个数?(提示 )
) 元/分钟和200元/分钟,规定省、市两个电视台为该公司所做的每分钟广告,能给公司带来的收益分别为0.3万元和0.2万元.问该公司如何分配在省、市两个电视台的广告时间,才能使公司的收益最大,最大收益是多少万元?
元/分钟和200元/分钟,规定省、市两个电视台为该公司所做的每分钟广告,能给公司带来的收益分别为0.3万元和0.2万元.问该公司如何分配在省、市两个电视台的广告时间,才能使公司的收益最大,最大收益是多少万元?
 在区间(0,1)内连续,且
在区间(0,1)内连续,且 .
.
