设f(x),g(x)分别是定义在R上的奇函数和偶函数,当x<0时,f′(x)g(x)+f(x)g′(x)>0,且g(-2)=0,则不等式f(x)g(x)>0的解集是( )
| A.(-2,0)∪(2,+∞) |
| B.(-2,0)∪(0,2) |
| C.(-∞,-2)∪(2,+∞) |
| D.(-∞,-2)∪(0,2) |
已知函数 ,则
,则 ( )
( )
A. | B. | C. | D. |
已知函数 在R上可导,且
在R上可导,且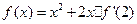 ,则
,则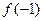 与
与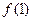 的大小关系为:
的大小关系为:
A.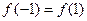 | B.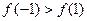 | C.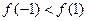 | D.不确定 |
函数f(x)=x3-3bx+3b在(0,1)内有极小值,则( )
| A.0<b<1 | B.b<1 | C.b>0 | D.b< |
若函数 的导数
的导数 ,则
,则 可以是
可以是
A. | B. | C. | D. |
函数 ,已知
,已知 在
在 时取极值,则a=
时取极值,则a=
| A.2 | B.3 | C.4 | D.5 |

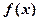 是定义在实数集
是定义在实数集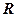 上的不恒为零的偶函数,
上的不恒为零的偶函数,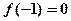 ,且对任意实数
,且对任意实数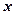 都
都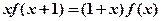 ,则
,则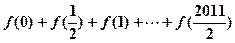 的值是
的值是 .
.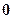

 .
. 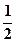
 .
. 
 .
.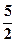
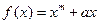 的导函数
的导函数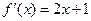 ,则数列
,则数列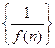 (n∈N*)的前n项和是
(n∈N*)的前n项和是 的图像与
的图像与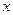 轴围成的封闭图形的面积为
轴围成的封闭图形的面积为 ,则
,则 的展开式中的常数项为( )
的展开式中的常数项为( )


