若函数
（
）的零点都在区间[-10,10]上，则使得方程
有正整数解的实数
的取值个数为 （ ）
| A．1; | B．2; | C．3； | D．4. |
(文)曲线f(x)＝x3＋x－2在p0点处的切线平行于直线y＝4x－1，则p0点的坐标为( )
| A．(－1,0) | B．(0，－2) |
| C．(－1，－4)或(1,0) | D．(1,4) |
(文)已知函数f(x)的导数为f′(x)，若f′(x)<0(a <x <b)且f(b)>0，则在(a，b)内必有( )
| A．f(x)＝0 | B．f(x)>0 | C．f(x)<0 | D．不能确定 |
若函数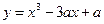
在
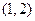内有极小值，则实数
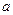的取值范围是（ ）
A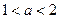． | B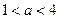． | C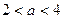． | D． |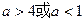
若函数
在
内有极小值，则实数
的取值范围是（ ）
A． | B． | C． | D． |
函数
(
,则（ ）
A． | B． | C． | D． 大小关系不能确定 |
设函数
的定义域为R+，若对于给定的正数K，定义函数
，则当函数
时，定积分
的值为
（ ）
| A．2ln2+2 | B．2ln2-1 | C．2ln2 | D．2ln2+1 |
已知函数
（
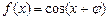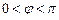）的导函数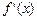
的图象如图所示，则
（ ）
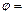A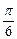．  | B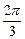． | C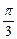． | D． |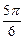
,（本小题满分12分）某工厂要建造一个长方体形无盖贮水池，其容积为4800m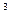
, 深为3 m。如果池底每平方米的造价为150元，池壁每平方米的造价为120元，怎样设计水池能使总造价最低？最低总造价是多少？