若f(1)=0,f(0)=f(1×0)=f(1)f(0)=0,所以f(1)=f(0)与已知条件“![]() ”矛盾所以f(1)≠0,因此f(1)=1,所以f(1)-1=0,1是函数y=f(x)-1的零点
”矛盾所以f(1)≠0,因此f(1)=1,所以f(1)-1=0,1是函数y=f(x)-1的零点
(2)因为f(1)=f[(-1)×(-1)]=f2(-1)=,所以f(-1)=±1,但若f(-1)=1,则f(-1)=f(1)与已知矛盾所以f(-1)不能等于1,只能等于-1。所以任x∈R,f(-x)=f(-1)f(x)=-f(x),因此函数是奇函数
已知某地每单位面积的菜地年平均使用氮肥量![]()
![]() 与每单位面积蔬菜年平均产量
与每单位面积蔬菜年平均产量![]() 之间有的关系如下数据:
之间有的关系如下数据:
| 年份 | x(kg) | y(t) |
| 1985 | 70 | 5.1 |
| 1986 | 74 | 6.0 |
| 1987 | 80 | 6.8 |
| 1988 | 78 | 7.8 |
| 1989 | 85 | 9.0 |
| 1990 | 92 | 10.2 |
| 1991 | 90 | 10.0 |
| 1992 | 95 | 12.0 |
| 1993 | 92 | 11.5 |
| 1994 | 108 | 11.0 |
| 1995 | 115 | 11.8 |
| 1996 | 123 | 12.2 |
| 1997 | 130 | 12.5 |
| 1998 | 138 | 12.8 |
| 1999 | 145 | 13.0 |
(1)求x与y之间的相关系数,并检验是否线性相关;
(2)若线性相关,则求蔬菜产量y与使用氮肥x之间的回归直线方程,并估计每单位面积施150kg时,每单位面积蔬菜的平均产量.
根据统计资料,我国能源生产自1986年以来发展很快.下面是我国能源生产总量(单位:亿吨标准煤)的几个统计数据:
| 年份 | 1986 | 1991 | 1996 | 2001 |
| 产量 | 8.6 | 10.4 | 12.9 | 16.1 |
根据有关专家预测,到2008年我国能源生产总量将达到19.4吨左右,则专家所选择的回归模型是下列四种模型中的那一种( )
A.![]() B.
B.![]()
C.![]() D.
D.![]()
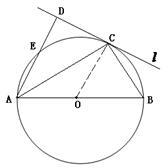 (选修4-1 几何证明选讲)(本题满分10分)
(选修4-1 几何证明选讲)(本题满分10分)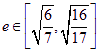 ,求椭圆长轴长的取值范围.
,求椭圆长轴长的取值范围.