如果点=的图象上,又在函数f(x)的反函数f-1(x)的图象上,那么a= ,b= .——青夏教育精英家教网——

如果点(1,2)既在函数f(x)=的图象上,又在函数f(x)的反函数f^-1(x)的图象上,那么a=_________,b=_________.

在给定的映射f:(x,y)→(x+y,xy)(x、y∈R)条件下,(7,10)的原象是_________.

定义在R上的函数y=f(x-1)是单调递减函数(如下图所示),给出四个结论,其中正确结论的个数是( )

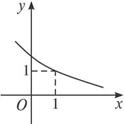
①f(0)=1 ②f(1)＜1 ③f^-1(1)=0 ④f^-1()＞0

A.1 B.2 C.3 D.4

已知f(x)=且f^-1(x-1)的图象的对称中心是(0,3),则a的值为( )

A. B.2 C. D.3

定义在R上的函数f(x)=-x-x³,设x₁+x₂≤0,给出下列不等式,其中正确不等式的序号是( )

①f(x₁)f(-x₁)≤0 ②f(x₂)f(-x₂)＞0 ③f(x₁)+f(x₂)≤f(-x₁)+f(-x₂) ④f(x₁)+f(x₂)≥f(-x₁)+f(-x₂)

A.①③ B.①④ C.②③ D.②④

函数y=a^x在［0,1］上的最大值与最小值的和为3,则a等于( )

A. B.2 C.4 D.

函数f(x)=x²+2(a-1)x+2在区间(-∞,4)上是减函数,则实数a的取值范围是( )

A.a≥3 B.a≤-3 C.a≤5 D.a=-3

已知函数f(x)=的定义域为R,则实数a的取值范围为( )

A.a＞ B.-12＜a＜0 C.-12＜a≤0 D.a≤

函数f(x)=(x≥2)的反函数f^-1(x)的图象为( )

设f、g都是由A到A的映射,其对应法则如下表(从上到下):

表1 映射f的对应法则

原象	1	2	3	4
象	3	4	2	1

表2 映射g的对应法则

原象	1	2	3	4
象	4	3	1	2

则与f［g(1)］相同的是( )

A.g［f(1)］ B.g［f(2)］ C.g［f(3)］ D.g［f(4)］

0 54877 54885 54891 54895 54901 54903 54907 54913 54915 54921 54927 54931 54933 54937 54943 54945 54951 54955 54957 54961 54963 54967 54969 54971 54972 54973 54975 54976 54977 54979 54981 54985 54987 54991 54993 54997 55003 55005 55011 55015 55017 55021 55027 55033 55035 55041 55045 55047 55053 55057 55063 55071 266669