设F1，F2分别是椭圆
x2
4
+y2=1的左、右焦点，P是第一象限内该椭圆上的一点，且PF1⊥PF2，求点P的横坐标为（　　）
A、1
B、
8
3
C、2
2
D、
2
6
3
设θ是△ABC的一个内角，且sinθ+cosθ=
7
13
，则x2sinθ-y2cosθ=1表示（　　）
A、焦点在x轴上的椭圆
B、焦点在y轴上的椭圆
C、焦点在x轴上的双曲线
D、焦点在y轴上的双曲线
已知椭圆G：
x24
+y2=1．过点（m，0）作圆x2+y2=1的切线I交椭圆G于A，B两点．
（Ⅰ）求椭圆G的焦点坐标和离心率；
（Ⅱ）将|AB|表示为m的函数，并求|AB|的最大值．
已知函数f(x)=(x-k)2e
x
k
．
（Ⅰ）求f（x）的单调区间；
（Ⅱ）若对于任意的x∈（0，+∞），都有f（x）≤
1
e
，求k的取值范围．
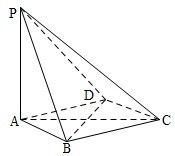精英家教网如图，在四棱锥P-ABCD中，PA⊥平面ABCD，底面ABCD是菱形，AB=2，∠BAD=60°．
（Ⅰ）求证：BD⊥平面PAC；
（Ⅱ）若PA=AB，求PB与AC所成角的余弦值；
（Ⅲ）当平面PBC与平面PDC垂直时，求PA的长．
17、在等差数列{an}中，若a10=0，则有等式：a1+a2+…+an=a1+a2+…+a19-n（n＜19）成立，类比上述性质，相应地，在等比数列{bn}中，若b9=1，则有等式
b1•b2•…•bn=b1•b2•…•b17-n（n＜17）
成立．
16、若函数f（x）=x3-3x在区间（a2-5，a）上有最大值，则实数a的取值范围是
-1＜a＜2
．
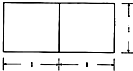精英家教网若一个底面是正三角形的三棱柱的正视图如图所示，其顶点都在一个球面上，则该球的表面积为
 
．
若不等式-4＜2x-3＜4，与不等式x2+px+q＜0的解集相同，则p+q的值为
 
．
f'（x）是函数f(x)=
1
3
x3-mx2+(m2-1)x+n的导函数，若函数y=f[f'（x）]在区间[m，m+1]上单调递减，则实数m的取值范围是（　　）
A、[-1，0]B、[0，1]
C、[-1，1]D、R
 0  33062  33070  33076  33080  33086  33088  33092  33098  33100  33106  33112  33116  33118  33122  33128  33130  33136  33140  33142  33146  33148  33152  33154  33156  33157  33158  33160  33161  33162  33164  33166  33170  33172  33176  33178  33182  33188  33190  33196  33200  33202  33206  33212  33218  33220  33226  33230  33232  33238  33242  33248  33256  266669 

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网