若0<a<1,函数f(x)=|logax|,m=f(
),n=f(
),p=f(3),则( )
| 1 |
| 4 |
| 1 |
| 2 |
| A、m>n>p |
| B、m>p>n |
| C、n>m>p |
| D、p>m>n |
函数y=
(x≥0)的图象上的点到A(
,
)的距离与到直线x=-
的距离之和的最小值为( )
| x |
| 5 |
| 4 |
| 3 |
| 5 |
| 4 |
A、
| ||
| B、3 | ||
| C、2 | ||
D、
|
与圆x2+(y-2)2=1相切,且在坐标轴上截距相等的直线有( )
| A、2条 | B、3条 | C、4条 | D、6条 |
已知函数f(x)=
x3-ax2-2x+1,设g(x)=(3a2-2)x,
(1)当a=
时,求函数f(x)的极值;
(2)如果函数f(x)与函数g(x)的图象有且仅有一个公共点,求实数a的取值范围.
0 31045 31053 31059 31063 31069 31071 31075 31081 31083 31089 31095 31099 31101 31105 31111 31113 31119 31123 31125 31129 31131 31135 31137 31139 31140 31141 31143 31144 31145 31147 31149 31153 31155 31159 31161 31165 31171 31173 31179 31183 31185 31189 31195 31201 31203 31209 31213 31215 31221 31225 31231 31239 266669
| 1 |
| 3 |
(1)当a=
| 1 |
| 2 |
(2)如果函数f(x)与函数g(x)的图象有且仅有一个公共点,求实数a的取值范围.
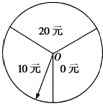 某商场为吸引顾客消费推出一项优惠活动.活动规则如下:消费每满100元可以转动如图所示的圆盘一次,其中O为圆心,且标有20元、10元、0元的三部分区域面积相等.假定指针停在任一位置都是等可能的.当指针停在某区域时,返相应金额的优惠券.(例如:某顾客消费了218元,第一次转动获得了20元,第二次获得了10元,则其共获得了30元优惠券.)顾客甲和乙都到商场进行了消费,并按照规则参与了活动.
某商场为吸引顾客消费推出一项优惠活动.活动规则如下:消费每满100元可以转动如图所示的圆盘一次,其中O为圆心,且标有20元、10元、0元的三部分区域面积相等.假定指针停在任一位置都是等可能的.当指针停在某区域时,返相应金额的优惠券.(例如:某顾客消费了218元,第一次转动获得了20元,第二次获得了10元,则其共获得了30元优惠券.)顾客甲和乙都到商场进行了消费,并按照规则参与了活动.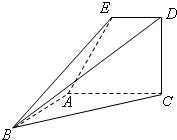 如图,已知直角梯形ACDE所在的平面垂直于平面ABC,∠BAC=∠ACD=90°,∠EAC=60°,AB=AC=AE.
如图,已知直角梯形ACDE所在的平面垂直于平面ABC,∠BAC=∠ACD=90°,∠EAC=60°,AB=AC=AE.