 如图,位于A处的信息中心获悉:在其正东方向相距40海里的B处有一艘渔船遇险,在原地等待营救.信息中心立即把消息告知在其南偏西30°、相距20海里的C处的乙船,现乙船朝北偏东θ的方向即沿直线CB前往B处救援,则cosθ=( )
如图,位于A处的信息中心获悉:在其正东方向相距40海里的B处有一艘渔船遇险,在原地等待营救.信息中心立即把消息告知在其南偏西30°、相距20海里的C处的乙船,现乙船朝北偏东θ的方向即沿直线CB前往B处救援,则cosθ=( )A、
| ||||
B、
| ||||
C、
| ||||
D、
|
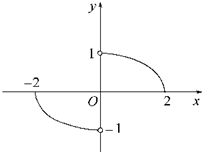 如图,函数y=f(x)的图象是中心在原点、焦点在x轴上的椭圆的两段弧,则不等式f(x)<f(-x)+x的解集为( )
如图,函数y=f(x)的图象是中心在原点、焦点在x轴上的椭圆的两段弧,则不等式f(x)<f(-x)+x的解集为( )A、{x|-
| ||||||||
B、{x|-2≤x<-
| ||||||||
C、{x|-2≤x<-
| ||||||||
D、{x|-
|
 如图,位于A处的信息中心获悉:在其正东方向相距40海里的B处有一艘渔船遇险,在原地等待营救.信息中心立即把消息告知在其南偏西30°、相距20海里的C处的乙船,现乙船朝北偏东θ的方向即沿直线CB前往B处救援,则cosθ=( )
如图,位于A处的信息中心获悉:在其正东方向相距40海里的B处有一艘渔船遇险,在原地等待营救.信息中心立即把消息告知在其南偏西30°、相距20海里的C处的乙船,现乙船朝北偏东θ的方向即沿直线CB前往B处救援,则cosθ=( )A、
| ||||
B、
| ||||
C、
| ||||
D、
|
 如图,函数y=f(x)的图象是中心在原点、焦点在x轴上的椭圆的两段弧,则不等式f(x)<f(-x)+x的解集为( )
如图,函数y=f(x)的图象是中心在原点、焦点在x轴上的椭圆的两段弧,则不等式f(x)<f(-x)+x的解集为( )A、{x|-
| ||||||||
B、{x|-2≤x<-
| ||||||||
C、{x|-2≤x<-
| ||||||||
D、{x|-
|