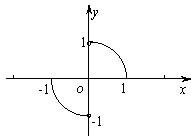
 函数y=f(x)的图象是圆心在原点的单位圆的两段弧(如图),则不等式f(x)<f(-x)+2x的解集为( )
函数y=f(x)的图象是圆心在原点的单位圆的两段弧(如图),则不等式f(x)<f(-x)+2x的解集为( )A、{x|-
| ||||||||
B、{x|-1≤x<-
| ||||||||
C、{x|-1≤x<-
| ||||||||
D、{x|-
|
命题甲“sinα>sinβ”,命题乙“α>β”,那么甲是乙成立的( )
| A、充分不必要条件 | B、必要不充分条件 | C、充要条件 | D、既不充分也不必要条件 |
 函数y=f(x)的图象是圆心在原点的单位圆的两段弧(如图),则不等式f(x)<f(-x)+2x的解集为( )
函数y=f(x)的图象是圆心在原点的单位圆的两段弧(如图),则不等式f(x)<f(-x)+2x的解集为( )A、{x|-
| ||||||||
B、{x|-1≤x<-
| ||||||||
C、{x|-1≤x<-
| ||||||||
D、{x|-
|
| A、充分不必要条件 | B、必要不充分条件 | C、充要条件 | D、既不充分也不必要条件 |