已知P是双曲线x2a2-y29=1右支上的一点.双曲线的一条渐近线方程为3x-y=0.设F1.F2分别为双曲线的左.右焦点.若|PF2|=3.则|PF1|= ．——青夏教育精英家教网——

已知P是双曲线

=1右支上的一点，双曲线的一条渐近线方程为3x-y=0、设F₁、F₂分别为双曲线的左、右焦点、若|PF₂|=3，则|PF₁|=

2、某班一次单元测试中，解答题部分的抽样成绩的茎叶图如下：则□内数字表示的某学生的原始成绩为

一组样本数据，容量为150，按从小到大的组序分成5个组，其频数如下表：那么，第5组的频率为

组号	1	2	3	4	5
频数	28	32	28	32	x

已知函数f（x）=

x³+ax²+bx，且f′（-1）=0．
（1）试用含a的代数式表示b，并求f（x）的单调区间；
（2）令a=-1，设函数f（x）在x₁，x₂（x₁＜x₂）处取得极值，记点M （x₁，f（x₁）），N（x₂，f（x₂）），P（m，f（m）），x₁＜m＜x₂，请仔细观察曲线f（x）在点P处的切线与线段MP的位置变化趋势，并解释以下问题：
（Ⅰ）若对任意的t∈（x₁，x₂），线段MP与曲线f（x）均有异于M，P的公共点，试确定t的最小值，并证明你的结论；
（Ⅱ）若存在点Q（n，f（n）），x≤n＜m，使得线段PQ与曲线f（x）有异于P、Q的公共点，请直接写出m的取值范围（不必给出求解过程）．

已知函数f（x）=x³+bx²+cx的导函数的图象关于直线x=2对称．
（1）求b的值；
（2）若f（x）在x=t处取得极小值，记此极小值为g（t），求g（t）的定义域和值域．

已知函数f（x）=-

x3+2ax²-3a²x+1，0＜a＜1．
（Ⅰ）求函数f（x）的极大值；
（Ⅱ）若x∈[1-a，1+a]时，恒有-a≤f′（x）≤a成立（其中f′（x）是函数f（x）的导函数），试确定实数a的取值范围．

设函数f（x）=ln（2x+3）+x²
（1）讨论f（x）的单调性；
（2）求f（x）在区间[-

]的最大值和最小值．

已知函数f（x）=x³-3ax²-bx，其中a，b为实数，
（1）若f（x）在x=1处取得的极值为2，求a，b的值；
（2）若f（x）在区间[-1，2]上为减函数，且b=9a，求a的取值范围．

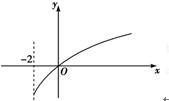已知函数f（x）的定义域为[-2，4]，且f（4）=f（-2）=1，f′（x）为f（x）的导函数，函数y=f′（x）的图象如图所示，则平面区域f（2a+b）＜1（a≥0，b≥0）所围成的面积是（　　）

3、如果函数y=f（x）的图象如图，那么导函数y=f′（x）的图象可能是（　　）

0 27666 27674 27680 27684 27690 27692 27696 27702 27704 27710 27716 27720 27722 27726 27732 27734 27740 27744 27746 27750 27752 27756 27758 27760 27761 27762 27764 27765 27766 27768 27770 27774 27776 27780 27782 27786 27792 27794 27800 27804 27806 27810 27816 27822 27824 27830 27834 27836 27842 27846 27852 27860 266669