【题目】某厂家准备在“6.18”举行促销活动,现根据近七年的广告费与销售量的数据确定此次广告费支出.广告费支出x(万元)和销售量y(万台)的数据如下:
年份 | 2013 | 2014 | 2015 | 2016 | 2017 | 2018 | 2019 |
广告费支出x | 1 | 2 | 4 | 6 | 11 | 13 | 19 |
销售量y | 1.8 | 3.0 | 4.0 | 4.2 | 5.0 | 5.3 | 5.4 |
(1)若用线性回归模型拟合y与x的关系,求出y关于x的线性回归方程(保留小数点后两位);
(2)若用![]() 模型拟合y与x的关系,可得回归方程
模型拟合y与x的关系,可得回归方程![]() ,经计算线性回归模型和该模型的R2分别约为0.774和0.888,请用R2说明选择哪个回归模型更好;
,经计算线性回归模型和该模型的R2分别约为0.774和0.888,请用R2说明选择哪个回归模型更好;
(3)已知利润z与x,y的关系为z=200y-x.根据(2)的结果,当广告费x=20时,求销售量及利润的预报值.
参考公式:回归直线![]() =
=![]() +
+![]() x的斜率和截距的最小二乘估计分别为
x的斜率和截距的最小二乘估计分别为![]() =
=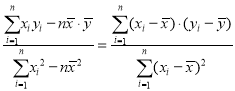 ,
,![]() .
.
参考数据:![]() ≈2.24,
≈2.24,![]() ,
, ![]()
【题目】为考察某种疫苗预防疾病的效果,进行动物试验,得到统计数据如下:现从所有试验动物中任取一只,取到“注射疫苗”动物的概率为![]() .
.
未发病 | 发病 | 总计 | |
未注射疫苗 | 20 | x | A |
注射疫苗 | 40 | y | B |
总计 | 60 | 40 | 100 |
(1)求2×2列联表中的数据x,y,A,B的值.
(2)能否在犯错误的概率不超过0.01的前提下认为疫苗有效?
附:![]()
临界值表:
P(K2≥k0) | 0.05 | 0.01 | 0.005 | 0.001 |
k0 | 3.841 | 6.635 | 7.879 | 10.828 |