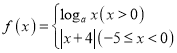【题目】每年春节,各地的餐馆都出现了用餐需预定的现象,致使一些人在没有预定的情况下难以找到用餐的餐馆,针对这种现象,专家对人们的用餐地点及性别作出调查,得到的情况如下表所示:
在家用餐 | 在餐馆用餐 | 总计 | |
男性 | 30 | ||
女性 | 40 | ||
总计 | 50 | 100 |
(1)完成上述![]() 列联表;
列联表;
(2)根据表中的数据,试通过计算判断是否有![]() 的把握说明用餐地点与性别有关?
的把握说明用餐地点与性别有关?
参考公式及数据: ,其中
,其中![]() .
.
P(K2≥k0) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
k0 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
【题目】为了了解某学校高二年级学生的物理成绩,从中抽取![]() 名学生的物理成绩(百分制)作为样本,按成绩分成5组:
名学生的物理成绩(百分制)作为样本,按成绩分成5组:![]() ,频率分布直方图如图所示,成绩落在
,频率分布直方图如图所示,成绩落在![]() 中的人数为20.
中的人数为20.

男生 | 女生 | 合计 | |
优秀 | |||
不优秀 | |||
合计 |
(1)求![]() 和
和![]() 的值;
的值;
(2)根据样本估计总体的思想,估计该校高二学生物理成绩的平均数![]() 和中位数
和中位数![]() ;
;
(3)成绩在80分以上(含80分)为优秀,样本中成绩落在![]() 中的男、女生人数比为1:2,成绩落在
中的男、女生人数比为1:2,成绩落在![]() 中的男、女生人数比为3:2,完成
中的男、女生人数比为3:2,完成![]() 列联表,并判断是否所有95%的把握认为物理成绩优秀与性别有关.
列联表,并判断是否所有95%的把握认为物理成绩优秀与性别有关.
参考公式和数据:
| 0.50 | 0.05 | 0.025 | 0.005 |
| 0.455 | 3.841 | 5.024 | 7.879 |
【题目】下表是某地某年月平均气温(华氏度):
月份 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
平均气温 | 21.4 | 26.0 | 36.0 | 48.8 | 59.1 | 68.6 | 73.0 | 71.9 | 64.7 | 53.5 | 39.8 | 27.7 |
以月份为x轴(![]() 月份
月份![]() ),以平均气温为y轴.
),以平均气温为y轴.
(1)用正弦曲线去拟合这些数据;
(2)估计这个正弦曲线的周期T和振幅A;
(3)下面三个函数模型中,哪一个最适合这些数据?
①![]() ;②
;②![]() ;③
;③![]() .
.