3.若函数f(x)=$\left\{\begin{array}{l}{x+{3}^{x}(x≤0)}\\{\frac{1}{3}{x}^{3}-4x+a(x>0)}\end{array}\right.$在定义域上只有一个零点,则实数a的取值范围是( )
| A. | a>$\frac{16}{3}$ | B. | a<$\frac{16}{3}$ | C. | a≥$\frac{16}{3}$ | D. | a≤$\frac{16}{3}$ |
1.设函数f(x)=2x,则如图所示的函数图象( )
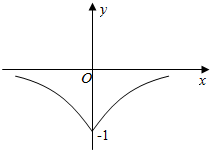

| A. | y=f(|x|) | B. | y=-|f(x)| | C. | y=-f(-|x|) | D. | y=f(-|x|) |
14.已知函数f(x)=ex-mx-exlnx+1,且定义域为(0,e],若函数f(x)在定义域内有两个极值点,则m的取值范围为( )
0 249848 249856 249862 249866 249872 249874 249878 249884 249886 249892 249898 249902 249904 249908 249914 249916 249922 249926 249928 249932 249934 249938 249940 249942 249943 249944 249946 249947 249948 249950 249952 249956 249958 249962 249964 249968 249974 249976 249982 249986 249988 249992 249998 250004 250006 250012 250016 250018 250024 250028 250034 250042 266669
| A. | [0,ee-2e] | B. | (0,ee-2e] | C. | (0,ee-2e) | D. | (ee-2e,+∞) |