题目内容
1.设函数f(x)=2x,则如图所示的函数图象( )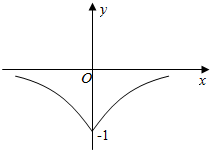
| A. | y=f(|x|) | B. | y=-|f(x)| | C. | y=-f(-|x|) | D. | y=f(-|x|) |
分析 由题意可知,图象关于y轴对称且图象位于y轴下方,函数值均为负值,说明函数为偶函数,再结合特殊值,利用排除法分析选项可得正确答案.
解答 解:因为当x=0时,y=-1,所以排除A,D.又因为函数的图象关于y轴对称,所以函数为偶函数,所以排除B,
所以C正确.
故选:C.
点评 本题考查了根据函数的图象求函数解析式的问题,指数函数图象的变换,难度不大,属于基础题.

练习册系列答案
 夺冠训练单元期末冲刺100分系列答案
夺冠训练单元期末冲刺100分系列答案 新思维小冠军100分作业本系列答案
新思维小冠军100分作业本系列答案 名师指导一卷通系列答案
名师指导一卷通系列答案
相关题目
7.在等差数列{an}中,Sp=q,Sq=q,Sp+q的值为( )
| A. | p+q | B. | -(p+q) | C. | p2-q2 | D. | p2+q2 |
12.已知等差数列{an}的前n项和Sn,满足a2013=S2013=2013,则a1=( )
| A. | -2014 | B. | -2013 | C. | -2012 | D. | -2011 |
6.函数f(x)=$\frac{{2{{cos}^2}(x-1)-x}}{x-1}$,其图象的对称中心是( )
| A. | (-1,1) | B. | (1,-1) | C. | (1,1) | D. | (0,-1) |
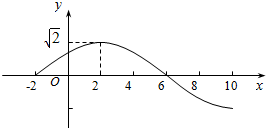 已知函数f(x)=Asin(ωx+ϕ)(A>0,ω>0,|ϕ|<$\frac{π}{2}$)的部分图象如图所示.
已知函数f(x)=Asin(ωx+ϕ)(A>0,ω>0,|ϕ|<$\frac{π}{2}$)的部分图象如图所示.