17.“ALS冰桶挑战赛”是一项社交网络上发起的筹款活动,活动规定:被邀请者要么在24小时内接受挑战,要么选择为慈善机构捐款(不接受挑战),并且不能重复参加该活动.若被邀请者接受挑战,则他需在网络上发布自己被冰水浇遍全身的视频内容,然后便可以邀请另外3个人参与这项活动.假设每个人接受挑战与不接受挑战是等可能的,且互不影响.
(Ⅰ)若某参与者接受挑战后,对其他3个人发出邀请,则这3个人中恰有2个人接受挑战的概率是多少?
(Ⅱ)为了解冰桶挑战赛与受邀者的性别是否有关,某调查机构进行了随机抽样调查,调查得到如下2×2列联表:
根据表中数据,是否有99%的把握认为“冰桶挑战赛与受邀者的性别有关”?
附:K2=$\frac{n(ad-bc)^{2}}{(a+b)(c+d)(a+c)(b+d)}$.
(Ⅰ)若某参与者接受挑战后,对其他3个人发出邀请,则这3个人中恰有2个人接受挑战的概率是多少?
(Ⅱ)为了解冰桶挑战赛与受邀者的性别是否有关,某调查机构进行了随机抽样调查,调查得到如下2×2列联表:
| 接受挑战 | 不接受挑战 | 合计 | |
| 男性 | 50 | 10 | 60 |
| 女性 | 25 | 15 | 40 |
| 合计 | 75 | 25 | 100 |
| P(K2≥k0) | 0.100 | 0.050 | 0.010 | 0.001 |
| k0 | 2.706 | 3.841 | 6.635 | 10.828 |
14.函数f(x)的定义域为R,f(0)=2,对任意x∈R,f(x)+f′(x)>1,则不等式exf(x)>ex+1,的解集是( )
| A. | {x|x>0} | B. | {x|x<0} | C. | {x|x<-1或x>1} | D. | {x|-1<x<1 } |
13.要证:a2+b2-1-a2b2≤0,只要证明( )
| A. | 2ab-1-a2b2≤0 | B. | ${a^2}+{b^2}-1-\frac{{{a^4}+{b^4}}}{2}≤0$ | ||
| C. | $\frac{{{{(a+b)}^2}}}{2}-1-{a^2}{b^2}≤0$ | D. | (a2-1)(b2-1)≥0 |
12.不等式(2+x)(x-3)<0的解集为( )
| A. | (-∞,-2)∪(3,+∞) | B. | (-2,3) | C. | [-2,3] | D. | (-3,2) |
9.某教师一天上3个班级的课,每班一节,如果一天共9节课,上午5节、下午4节,并且教师不能连上3节课(第5和第6节不算连上),那么这位教师一天的课的所有排法有( )
0 247345 247353 247359 247363 247369 247371 247375 247381 247383 247389 247395 247399 247401 247405 247411 247413 247419 247423 247425 247429 247431 247435 247437 247439 247440 247441 247443 247444 247445 247447 247449 247453 247455 247459 247461 247465 247471 247473 247479 247483 247485 247489 247495 247501 247503 247509 247513 247515 247521 247525 247531 247539 266669
| A. | 474种 | B. | 77种 | C. | 464种 | D. | 79种 |
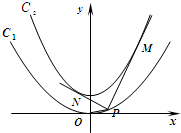 如图,已知抛物线C1:x2=2py的焦点在抛物线C2:y=$\frac{1}{2}$x2+$\frac{1}{4}$上.
如图,已知抛物线C1:x2=2py的焦点在抛物线C2:y=$\frac{1}{2}$x2+$\frac{1}{4}$上.