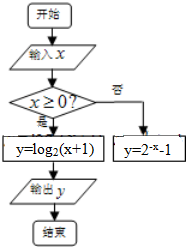
7．已知函数f(x)=sin2x-|sinx|-|cosx|的值域为[-1-$\sqrt{2}$.1-$\sqrt{2}$]．——青夏教育精英家教网——

7．已知函数f（x）=sin2x-|sinx|-|cosx|（x∈R），则f（x）的值域为[-1-$\sqrt{2}$，1-$\sqrt{2}$]．

6．执行如图所示的程序框图，如果输入的x∈[-1，3]，则输出的y属于（　　）

5．设全集U={x∈R|x≥0}，函数f（x）=$\sqrt{1-lgx}$的定义域为M，则∁_UM为（　　）

（10，+∞）∪{0}

（10，+∞）

4．已知数列{a_n}满足a_n+1-a_n=2（n∈N^*），且a₁，a₄，a₁₃成等比数列．
（Ⅰ）求数列{a_n}的通项公式及前n项和；
（Ⅱ）设数列$\left\{\frac{1}{{S}_{n}}\right\}$的前n项和为T_n，证明：${T}_{n}≤\frac{3}{4}$（n∈N^*）．

3．在△ABC中，三内角A，B，C的对边分别为a，b，c且a²=b²+c²+bc，a=$\sqrt{3}$，S为△ABC的面积，则S+$\sqrt{3}$cosBcosC的最大值为（　　）

2．将函数y=f（x）的图象向右平移$\frac{π}{2}$个单位得到函数y=cos2x的图象，再将函数y=f（x）的横坐标伸长到原来的2倍，纵坐标不变，得到函数y=g（x）的图象，则g（x）=（　　）

1．直线l过抛物线y²=x的焦点F，交抛物线于A、B两点，且点A在x轴上方．若直线l的倾斜角θ≥$\frac{π}{4}$，则|FA|的取值范围是（$\frac{1}{4}$，1+$\frac{\sqrt{2}}{2}$]．

20．在△ABC中，内角A、B、C的对边分别为a，b，c．若cosB=$\frac{1}{4}，sinC=2sinA，{S_{△ABC}}=\frac{{\sqrt{15}}}{4}$，则b=（　　）

19．已知f（x）是定义在R上的奇函数，f（-1）=-1，且当x＞0时，有xf′（x）＞f（x），则不等式f（x）＞x的解集是（　　）

（-1，0）∪（1，+∞）

（-∞，-1）∪（1，+∞）

18．函数f（x）的部分图象如图所示，则f（x）的解析式可以是（　　）

f（x）=x+sinx

f（x）=x•sinx

f（x）=x•cosx

f（x）=x（x-$\frac{π}{2}$）（x-$\frac{3π}{2}$）

0 246803 246811 246817 246821 246827 246829 246833 246839 246841 246847 246853 246857 246859 246863 246869 246871 246877 246881 246883 246887 246889 246893 246895 246897 246898 246899 246901 246902 246903 246905 246907 246911 246913 246917 246919 246923 246929 246931 246937 246941 246943 246947 246953 246959 246961 246967 246971 246973 246979 246983 246989 246997 266669