17．设等比数列{an}的前n项和为Sn，S4=10，S12=130，则S16为（ ）
| A． | 400 | B． | -510 | C． | 400或-510 | D． | 270 |
16．如图所示，程序框图的功能是（ ）
| A． | 求{$\frac{1}{n}$}前10项和 | B． | 求{$\frac{1}{2n}$}前10项和 | C． | 求{$\frac{1}{n}$}前11项和 | D． | 求{$\frac{1}{2n}$}前11项和 |
15．
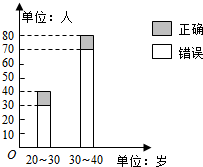“开门大吉”是某电视台推出的游戏节目．选手面对1～8号8扇大门，依次按响门上的门铃，门铃会播放一段音乐（将一首经典流行歌曲以单音色旋律的方式演绎），选手需正确回答出这首歌的名字，方可获得该扇门对应的家庭梦想基金．在一次场外调查中，发现参赛选手多数分为两个年龄段：20～30；30～40（单位：岁），其猜对歌曲名称与否的人数如图所示．
（1）写出2×2列联表；判断是否有90%的把握认为猜对歌曲名称与否和年龄有关；说明你的理由；（下面的临界值表供参考）
（2）现计划在这次场外调查中按年龄段选取9名选手，并抽取3名幸运选手，求3名幸运选手中在20～30岁之间的人数的分布列和数学期望．
（参考公式：${K^2}=\frac{{n{{（ad-bc）}^2}}}{（a+b）（c+d）（a+c）（b+d）}$其中n=a+b+c+d）
“开门大吉”是某电视台推出的游戏节目．选手面对1～8号8扇大门，依次按响门上的门铃，门铃会播放一段音乐（将一首经典流行歌曲以单音色旋律的方式演绎），选手需正确回答出这首歌的名字，方可获得该扇门对应的家庭梦想基金．在一次场外调查中，发现参赛选手多数分为两个年龄段：20～30；30～40（单位：岁），其猜对歌曲名称与否的人数如图所示．（1）写出2×2列联表；判断是否有90%的把握认为猜对歌曲名称与否和年龄有关；说明你的理由；（下面的临界值表供参考）
| P（K2≥k0） | 0.10 | 0.05 | 0.010 | 0.005 |
| k0 | 2.706 | 3.841 | 6.635 | 7.879 |
（参考公式：${K^2}=\frac{{n{{（ad-bc）}^2}}}{（a+b）（c+d）（a+c）（b+d）}$其中n=a+b+c+d）
10．已知：a，b，c，d满足：log${\;}_{\frac{1}{2}}$a=3a，log${\;}_{\frac{1}{2}}$b=2b，$\frac{1}{{3}^{c}}$=log2c，$\frac{1}{{2}^{d}}$=log2d．则a，b，c，d的大小关系是（ ）
| A． | a＞b＞c＞d | B． | a＜b＜c＜d | C． | a＞b＞d＞c | D． | b＞a＞c＞d |
9．若$\frac{1}{27}$≤x≤9，则f（x）=log3$\frac{x}{27}$•log3（3x）（ ）
| A． | 有最小值-$\frac{32}{9}$，最大值-3 | B． | 有最小-4，最大值12 | ||
| C． | 有最小值-$\frac{32}{9}$，无最大值 | D． | 无最小值，有最大值12 |
8．已知函数f（x）=$\frac{x（{a}^{x}-1）}{{a}^{x}+1}$（a＞0，a≠1），则（ ）
0 246784 246792 246798 246802 246808 246810 246814 246820 246822 246828 246834 246838 246840 246844 246850 246852 246858 246862 246864 246868 246870 246874 246876 246878 246879 246880 246882 246883 246884 246886 246888 246892 246894 246898 246900 246904 246910 246912 246918 246922 246924 246928 246934 246940 246942 246948 246952 246954 246960 246964 246970 246978 266669
| A． | 函数f（x）在（0，+∞）上是增函数 | B． | 函数f（x）在（0，+∞）上是减函数 | ||
| C． | 函数f（x）是奇函数 | D． | 函数f（x）是偶函数 |