1. 我国南宋数学家秦九韶(约公园1202-1261年)给出了求n(n∈N*)次多项式anxn+an-1xn-1+…+a1x+a0的值的一种简捷算法,改算法被后人命名为“秦九韶算法”,其程序框图如图所示.当x=0.4时,多项式x4+0.6x3+x2-2.56x+1的值为( )
我国南宋数学家秦九韶(约公园1202-1261年)给出了求n(n∈N*)次多项式anxn+an-1xn-1+…+a1x+a0的值的一种简捷算法,改算法被后人命名为“秦九韶算法”,其程序框图如图所示.当x=0.4时,多项式x4+0.6x3+x2-2.56x+1的值为( )
 我国南宋数学家秦九韶(约公园1202-1261年)给出了求n(n∈N*)次多项式anxn+an-1xn-1+…+a1x+a0的值的一种简捷算法,改算法被后人命名为“秦九韶算法”,其程序框图如图所示.当x=0.4时,多项式x4+0.6x3+x2-2.56x+1的值为( )
我国南宋数学家秦九韶(约公园1202-1261年)给出了求n(n∈N*)次多项式anxn+an-1xn-1+…+a1x+a0的值的一种简捷算法,改算法被后人命名为“秦九韶算法”,其程序框图如图所示.当x=0.4时,多项式x4+0.6x3+x2-2.56x+1的值为( )| A. | 0.2 | B. | 1.58944 | C. | 1.26176 | D. | 2.248 |
17.由圆心与弦(非直径)中点的连线垂直于弦,想到球心与截面圆(不经过球心的小截面圆)圆心的连线垂直于截面,用的是( )
| A. | 类比推理 | B. | 三段论推理 | C. | 归纳推理 | D. | 传递性推理 |
15.已知向量$\overrightarrow{a}$、$\overrightarrow{b}$满足|$\overrightarrow{a}$|=3,|$\overrightarrow{b}$|=2,($\overrightarrow{a}$-$\overrightarrow{b}$)•($\overrightarrow{a}$+2$\overrightarrow{b}$)=-2,则$\overrightarrow{a}$与$\overrightarrow{b}$的夹角为( )
| A. | $\frac{2π}{3}$ | B. | $\frac{π}{3}$ | C. | $\frac{5π}{6}$ | D. | $\frac{π}{6}$ |
14.执行图示的程序框图,则输出的结果为( )
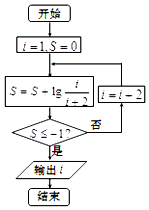

| A. | 7 | B. | 9 | C. | 10 | D. | 11 |
13. 如图,1,2,3,4号是四盏灯,A、B、C是控制这四盏灯的三个开关,若开关A控制2,3,4号灯(即按一下开关A,2,3,4号四盏灯亮,再按一下开关A,2,3,4号四盏灯熄灭),开关B控制1,3,4号灯,开关C控制1,2,4号灯.开始时,四盏灯都亮着,那么下面的说法正确的是( )
如图,1,2,3,4号是四盏灯,A、B、C是控制这四盏灯的三个开关,若开关A控制2,3,4号灯(即按一下开关A,2,3,4号四盏灯亮,再按一下开关A,2,3,4号四盏灯熄灭),开关B控制1,3,4号灯,开关C控制1,2,4号灯.开始时,四盏灯都亮着,那么下面的说法正确的是( )
0 241007 241015 241021 241025 241031 241033 241037 241043 241045 241051 241057 241061 241063 241067 241073 241075 241081 241085 241087 241091 241093 241097 241099 241101 241102 241103 241105 241106 241107 241109 241111 241115 241117 241121 241123 241127 241133 241135 241141 241145 241147 241151 241157 241163 241165 241171 241175 241177 241183 241187 241193 241201 266669
 如图,1,2,3,4号是四盏灯,A、B、C是控制这四盏灯的三个开关,若开关A控制2,3,4号灯(即按一下开关A,2,3,4号四盏灯亮,再按一下开关A,2,3,4号四盏灯熄灭),开关B控制1,3,4号灯,开关C控制1,2,4号灯.开始时,四盏灯都亮着,那么下面的说法正确的是( )
如图,1,2,3,4号是四盏灯,A、B、C是控制这四盏灯的三个开关,若开关A控制2,3,4号灯(即按一下开关A,2,3,4号四盏灯亮,再按一下开关A,2,3,4号四盏灯熄灭),开关B控制1,3,4号灯,开关C控制1,2,4号灯.开始时,四盏灯都亮着,那么下面的说法正确的是( )| A. | 只需要按开关A,C可以将四盏灯全部熄灭 | |
| B. | 只需要按开关B,C可以将四盏灯全部熄灭 | |
| C. | 按开关A,B,C可以将四盏灯全部熄灭 | |
| D. | 按开关A,B,C无法将四盏灯全部熄灭 |
 执行如图所示的程序框图,若输出的y=6,则输入的x=-6或3.
执行如图所示的程序框图,若输出的y=6,则输入的x=-6或3. 今年暑假,小明一家准备从A城到G城自驾游,他规划了一个路线时间图,箭头上的数字表示所需的时间(单位:小时),那么从A城到G城所需的最短时间为10小时.
今年暑假,小明一家准备从A城到G城自驾游,他规划了一个路线时间图,箭头上的数字表示所需的时间(单位:小时),那么从A城到G城所需的最短时间为10小时.