7.某旅行社为调查市民喜欢“人文景观”景点是否与年龄有关,随机抽取了55名市民,得到数据如下表:
(1)判断是否在犯错误的概率不超过0.5%的前提下认为喜欢“人文景观”景点与年龄有关?
(2)用分层抽样的方法从喜欢“人文景观”景点的市民中随机抽取6人作进一步调查,将这6位市民作为一个样本,从中任选2人,求恰有1位“大于40岁”的市民和1位“20岁至40岁”的市民的概率.
参考公式:${K^2}=\frac{{n{{(ad-bc)}^2}}}{(a+b)(c+d)(a+c)(b+d)}$,其中n=a+b+c+d为样本容量.
参考数据:
0 238959 238967 238973 238977 238983 238985 238989 238995 238997 239003 239009 239013 239015 239019 239025 239027 239033 239037 239039 239043 239045 239049 239051 239053 239054 239055 239057 239058 239059 239061 239063 239067 239069 239073 239075 239079 239085 239087 239093 239097 239099 239103 239109 239115 239117 239123 239127 239129 239135 239139 239145 239153 266669
| 喜欢 | 不喜欢 | 总计 | |
| 大于40岁 | 20 | 5 | 25 |
| 20岁至40岁 | 10 | 20 | 30 |
| 总计 | 30 | 25 | 55 |
(2)用分层抽样的方法从喜欢“人文景观”景点的市民中随机抽取6人作进一步调查,将这6位市民作为一个样本,从中任选2人,求恰有1位“大于40岁”的市民和1位“20岁至40岁”的市民的概率.
参考公式:${K^2}=\frac{{n{{(ad-bc)}^2}}}{(a+b)(c+d)(a+c)(b+d)}$,其中n=a+b+c+d为样本容量.
参考数据:
| P(K2≥k0) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k0 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
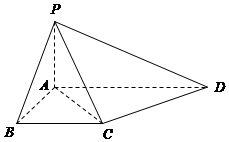 AD∥BC,∠ABC=∠PAD=90°,侧面PAD⊥底面ABCD.若 PA=AB=BC=$\frac{1}{2}$AD.
AD∥BC,∠ABC=∠PAD=90°,侧面PAD⊥底面ABCD.若 PA=AB=BC=$\frac{1}{2}$AD.