如果一条直线与一个平面平行，那么称此直线与平面构成一个“平行线面组”，在一个长方体中，由两个顶点确定的直线与含有四个顶点的平面构成的“平行线面组”的个数是( )
A．60 B．48
C．36 D．24
某城市随机抽取一年(365天)内100天的空气质量指数API的监测数据，结果统计如下：
| API | [0,50] | (50,100] | (100,150] | (150,200] | (200,250] | (250,300] | >300 |
| 空气 质量 | 优 | 良 | 轻微 污染 | 轻度 污染 | 中度 污染 | 中重度 污染 | 重度 污染 |
| 天数 | 4 | 13 | 18 | 30 | 9 | 11 | 15 |
(1)若某企业每天由空气污染造成的经济损失S(单位：元)与空气质量指数API(记为w)的关系为：
S＝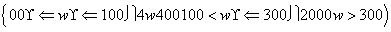
试估计在本年度内随机抽取一天，该天经济损失S大于200元且不超过600元的概率；
(2)若本次抽取的样本数据有30天是在供暖季，其中有8天为重度污染．完成下面2×2列联表，并判断能否有95%的把握认为该市本年空气重度污染与供暖有关？
|
| 非重度污染 | 重度污染 | 合计 |
| 供暖季 | |||
| 非供暖季 | |||
| 合计 |
|
| 100 |
附：
| P(K2≥k0) | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k0 | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
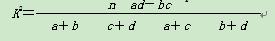
有甲、乙两个班级进行数学考试，按照大于或等于85分为优秀，85分以下为非优秀统计成绩后，得到如下的2×2列联表．已知从全部210人中随机抽取1人为优秀的概率为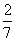
.
|
| 优秀 | 非优秀 | 总计 |
| 甲班 | 20 | ||
| 乙班 |
| 60 | |
| 合计 |
|
| 210 |
(1)请完成上面的2×2列联表，并判断若按99%的可靠性要求，能否认为“成绩与班级有关”；
(2)从全部210人中有放回地抽取3次，每次抽取1人，记被抽取的3人中的优秀人数为ξ，若每次抽取的结果是相互独立的，求ξ的分布列及数学期望E(ξ)．
附：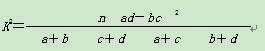
| P(K2≥k) | 0.05 | 0.01 |
| k | 3.841 | 6.635 |
某人研究中学生的性别与成绩、视力、智商、阅读量这4个变量的关系，随机抽查52名中学生，得到统计数据如表1至表4，则与性别有关联的可能性最大的变量是( )
表1
| 成绩 性别 | 不及格 | 及格 | 总计 |
| 男 | 6 | 14 | 20 |
| 女 | 10 | 22 | 32 |
| 总计 | 16 | 36 | 52 |
表2
| 视力 性别 | 好 | 差 | 总计 |
| 男 | 4 | 16 | 20 |
| 女 | 12 | 20 | 32 |
| 总计 | 16 | 36 | 52 |
表3
| 智商 性别 | 偏高 | 正常 | 总计 |
| 男 | 8 | 12 | 20 |
| 女 | 8 | 24 | 32 |
| 总计 | 16 | 36 | 52 |
表4
| 阅读量 性别 | 丰富 | 不丰富 | 总计 |
| 男 | 14 | 6 | 20 |
| 女 | 2 | 30 | 32 |
| 总计 | 16 | 36 | 52 |
A．成绩 B．视力
C．智商 D．阅读量
为了解篮球爱好者小李的投篮命中率与打篮球时间之间的关系，下表记录了小李某月1号到5号每天打篮球时间x(单位：小时)与当天投篮命中率y之间的关系：
| 时间x | 1 | 2 | 3 | 4 | 5 |
| 命中率y | 0.4 | 0.5 | 0.6 | 0.6 | 0.4 |
小李这5天的平均投篮命中率为________；用线性回归分析的方法，预测小李该月6号打6小时篮球的投篮命中率为________．