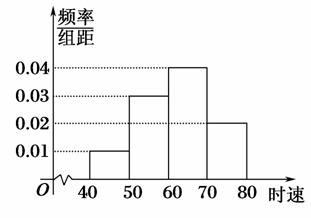
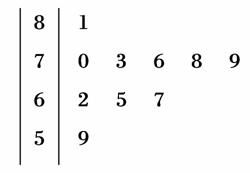
对于下列表格所示五个散点，已知求得的线性回归方程为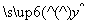＝0.8x－155，则实数m的值为(　　)

A.8                                     B．8.2

C．8.4                                  D．8.5

下面是2×2列联表：

则表中a，b的值分别为(　　)

A．94,72                                B．52,50

C．52,74                                D．74,52

对四组数据进行统计，获得以下散点图，关于其相关系数的比较，正确的是(　　)

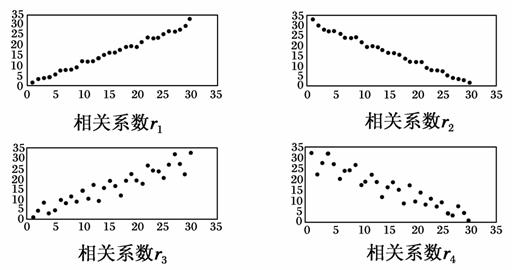
A．r₂<r₄<0<r₃<r₁                          B．r₄<r₂<0<r₁<r₃

C．r₄<r₂<0<r₃<r₁                          D．r₂<r₄<0<r₁<r₃

从某校随机抽取100名学生，获得了他们一周课外阅读时间(单位：小时)的数据，整理得到数据分组及频数分布表和频率分布直方图.

续表

(1)从该校随机选取一名学生，试估计这名学生该周课外阅读时间少于12小时的概率；

(2)求频率分布直方图中的a，b的值；

(3)假设同一组中的每个数据可用该组区间的中点值代替，试估计样本中的100名学生该周课外阅读时间的平均数在第几组．(只需写出结论)

关于统计数据的分析，有以下5种说法：

①一组数不可能有两个众数；

②将一组数据中的每个数据都减去同一个数后，方差没有变化；

③调查影剧院中观众观看感受时，从50排(每排人数相同)中任意取一个排的人参加调查，属于分层抽样；

④一组数据的方差一定是正数；

⑤如图是随机抽取的200辆汽车通过某一段公路时的时速分布直方图，根据这个直方图，可以得到时速在[50,60)的汽车大约是60辆．

这5种说法中错误的是________．(填序号)

一个样本容量为10的样本数据，它们组成一个公差不为0的等差数列{a_n}，若a₃＝8，且a₁，a₃，a₇成等比数列，则此样本的平均数和中位数分别是(　　)

A．13,12                                B．13,13

C．12,13                                D．13,14

如图是依据某城市年龄在20岁到45岁在居民上网情况调查而绘制的频率分布直方图，现已知年龄在[30,35)，[35,40)，[40,45]的上网人数呈现递减的等差数列分布，则年龄在[35,40)的网民出现的频率为(　　)

A．0.04                                 B．0.06

C．0.2                                  D．0.3

为了增强学生的环保意识，某中学随机抽取了50名学生举行了一次环保知识竞赛，并将本次竞赛的成绩(得分均为整数，满分100分)整理，制成下表：

(1)作出被抽查学生成绩的频率分布直方图；

(2)若从成绩在[40,50)中选一名学生，从成绩在[90,100]中选2名学生，共3名学生召开座谈会，求[40,50)组中学生A₁和[90,100]组中学生B₁同时被选中的概率．

已知某单位有50名职工，现在从中抽取10名职工，将全体职工随机按1～50编号，并按编号顺序平均分成10组，按各组内抽取的编号依次增加5进行系统抽样．

(1)若第5组抽出的号码为22，写出所有被抽出职工的号码；

(2)分别统计这10名职工的体重(单位：kg)，获得体重数据的茎叶图如图所示，求该样本的方差；

(3)在(2)的条件下，从这10名职工中随机抽取两名体重不轻于73 kg(≥73 kg)的职工，求体重为76 kg的职工被抽取到的概率．