已知数列: ,依它的前10项的规律,这个数列的第2010项a2010满足( )
,依它的前10项的规律,这个数列的第2010项a2010满足( )
|
| A. |
| B. |
| C. | 1≤a2010≤10 | D. | a2010>10 |
在数列{an}中,若an2﹣an﹣12=p(n≥2,n∈N*,p为常数),则称{an}为“等方差数列”,下列是对“等方差数列”的判断;
①若{an}是等方差数列,则{an2}是等差数列;②{(﹣1)n}是等方差数列;
③若{an}是等方差数列,则{akn}(k∈N*,k为常数)也是等方差数列;
④若{an}既是等方差数列,又是等差数列,则该数列为常数列.
其中正确命题序号为( )
|
| A. | ①②③ | B. | ①②④ | C. | ①②③④ | D. | ②③④ |
设f(x)是定义在R上恒不为0的函数,对任意x,y∈R,都有f(x)•f(y)=f(x+y),若a1= ,an=f(n)(n为常数),则数列{an}的前n项和Sn的取值范围是( )
,an=f(n)(n为常数),则数列{an}的前n项和Sn的取值范围是( )
|
| A. | [ | B. | [ | C. | [ | D. | [ |
若数列{an}满足:存在正整数T,对于任意正整数n都有an+T=an成立,则称数列{an}为周期数列,周期为T.已知数列{an}满足a1=m(m>0),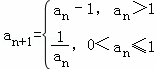 则下列结论中错误的是( )
则下列结论中错误的是( )
|
| A. | 若a3=4,则m可以取3个不同的值 |
|
| B. | 若 |
|
| C. | ∀T∈N*且T≥2,存在m>1,使得{an}是周期为T的数列 |
|
| D. | ∃m∈Q且m≥2,使得数列{an}是周期数列 |


 ,则数列{an}是周期为3的数列
,则数列{an}是周期为3的数列 的各项均为正数,公比
的各项均为正数,公比 ≠1,设
≠1,设 =
=

 ,
, =
= ,则
,则 ,
, =
= ,则
,则
 ( )
( ) B.
B. C.
C. D.
D.
 满足:
满足: 且
且 ,
, 是数列
是数列 项和。则满足
项和。则满足 的正整数对
的正整数对 的个数为( )个A.
的个数为( )个A. B.
B. C.
C. D.
D.
 }中,各项都是正数,且a1,
}中,各项都是正数,且a1,  =( )
=( ) B.1+
B.1+ 成等差数列,则下列不等式一定成立的是( )
成等差数列,则下列不等式一定成立的是( ) B.
B. C.
C. D.
D.
 。下列命题中真命题是 ( )
。下列命题中真命题是 ( ) n∈N*总有
n∈N*总有 ∥
∥ 成立,则数列{an}是等差数列 B.若
成立,则数列{an}是等差数列 B.若