函数的零点所在的大致区间是 (   )

   A .              B.            C. 和       D.

椭圆上有一点P到左焦点的距离是4，则点p到右焦点的距离是（   ）

   A.3                B.、4              C.5             D.6

 已知命题：，，那么命题为    (    )

   A.，             B.，

   C.，             D.，

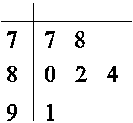
2013年12月21日上午10时，石家庄首次启动重污染天气Ⅱ级应急响应，正式实施机动车尾号限行，当天某报社为了解公众对“车辆限行”的态度，随机抽查了50人，将调查情况进行整理后制成下表：

(1)完成被调查人员的频率分布直方图；

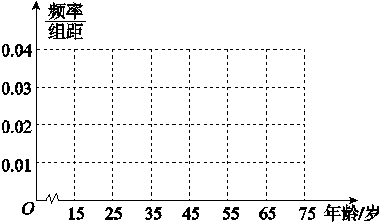
(2)若从年龄在[15,25)，[25,35)的调查者中各随机选取两人进行追踪调查，记选中的4人中不赞成“车辆限行”的人数为ξ，求随机变量ξ的分布列和数学期望．

一次考试中，五名学生的数学、物理成绩如下表所示：

(1)要从5名学生中选2人参加一项活动，求选中的学生中至少有一人的物理成绩高于90分的概率；

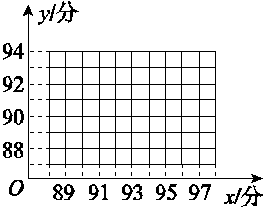
(2)根据上表数据，用变量y与x的相关系数和散点图说明物理成绩y与数学成绩x之间线性相关关系的强弱．如果具有较强的线性相关关系，求y与x的线性回归方程(系数精确到0.01)；如果不具有线性相关关系，请说明理由．

参考公式：

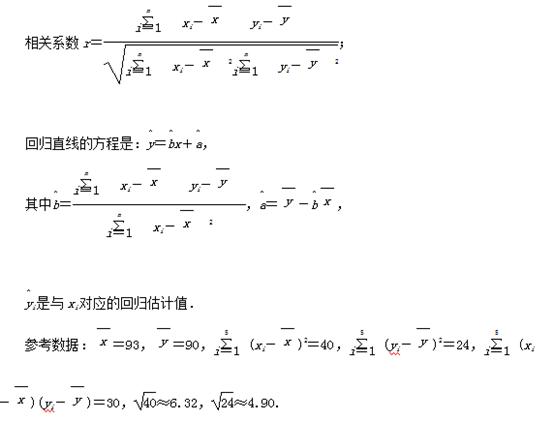
随机询问某大学40名不同性别的大学生在购买食物时是否读营养说明，得到如下列联表：

性别与是否读营养说明列联表

(1)根据以上列联表进行独立性检验，能否在犯错误的概率不超过0.01的前提下认为性别与是否读营养说明之间有关系？

(2)从被询问的16名不读营养说明的大学生中，随机抽取2名学生，求抽到男生人数ξ的分布列及其均值(即数学期望)．

为组织好“市九运会”，组委会征集了800名志愿者，现对他们的年龄抽样统计后，得到如图所示的频率分布直方图，但是年龄在[25,30)内的数据不慎丢失，依据此图可得：

(1)年龄在[25,30)内对应小长方形的高度为________；

(2)这800名志愿者中年龄在[25,35)内的人数为________．

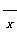在一次演讲比赛中，6位评委对一名选手打分的茎叶图如图(1)所示，若去掉一个最高分和一个最低分，得到一组数据x_i(1≤i≤4)，在如图(2)所示的程序框图中，是这4个数据的平均数，则输出的v的值为________．

(1)

(2)

某学校共有师生3 200人，现用分层抽样的方法，从所有师生中抽取一个容量为160的样本，已知从学生中抽取的人数为150，那么该学校的教师人数是________．

假设要考察某公司生产的500克袋装牛奶的三聚氰胺是否超标，现从800袋牛奶中抽取60袋进行检验，利用随机数表抽取样本时，先将800袋牛奶按000,001，…，799进行编号，如果从随机数表第7行第8列的数开始向右读，则得到的第4个样本个体的编号是________．(下面摘取了随机数表第7行至第9行)

84 42 17 53 31 　 57 24 55 06 88　  77 04 74 47 67  　21 76 33 50 25 　   83 92 12 06 76

63 01 63 78 59　  16 95 56 67 19　  98 10 50 71 75 　 12 86 73 58 07  　  44 39 52 38 79

33 21 12 34 29 　 78 64 56 07 82　  52 42 07 44 38 　 15 51 00 13 42   　 99 66 02 79 54