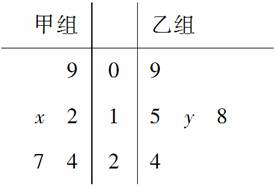
为了参加2013贵州省高中篮球比赛,某中学决定从四个篮球较强的班级的篮球队员中选出12人组成男子篮球队,代表该地区参赛,四个篮球较强的班级篮球队员人数如下表:
| 班级 | 高三(7)班 | 高三(17)班 | 高二(31)班 | 高二(32)班 |
| 人数 | 12 | 6 | 9 | 9 |
(1)现采取分层抽样的方法是从这四个班中抽取运动员,求应分别从这四个班抽出的队员人数;
(2)该中学篮球队奋力拼搏,获得冠军.若要从高三(7)班和高三(17)班抽出的队员中选出两位队员作为冠军的代表发言,求选出的两名队员来自同一班的概率.
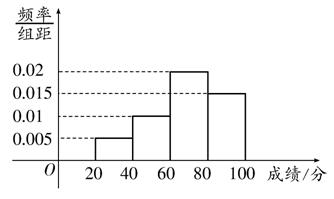
某高校在2013年的自主招生考试成绩中随机抽取100名学生的笔试成绩,按成绩分组,得到的频率分布表如下表所示.
| 编号 | 分组 | 频数 | 频率 |
| 第一组 | [160,165) | 5 | 0.050 |
| 第二组 | [165,170) | x | 0.350 |
| 第三组 | [170,175) | 30 | y |
| 第四组 | [175,180) | 20 | 0.200 |
| 第五组 | [180,185] | 10 | 0.100 |
| 合计 | 100 | 1 |

(1)求出频率分布表中x、y的值,再在答题纸上完成下列频率分布直方图;
(2)为了能选拔出最优秀的学生,高校决定在笔试成绩高的第3、4、5组中用分层抽样抽取6名学生进入第二轮面试,求第3、4、5组每组各抽取多少名学生进入第二轮面试;
(3)在(2)的前提下,学校决定在6名学生中随机抽取2名学生接受A考官进行面试,求第4组至少有一名学生被A考官面试的概率.
郑州市某学校为了促进教师业务能力的提升,决定组织部分学科教师参加市达标课活动,规定用分层抽样的方法,先从语文、英语、政治、历史、地理学科中抽取部分教师参加,各学科教师人数分布表如下:
| 学科 | 语文 | 英语 | 政治 | 历史 | 地理 |
| 人数 | 24 | 24 | 15 | 12 | 9 |
| 抽取人数 | 8 | 8 | a | b | c |
(1)求a、b、c的值;
(2)若要在历史和地理学科已抽取的教师中,随机选取两名教师参加市教学技能竞赛,求抽取的两位教师全是历史教师的概率.

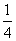 (x
(x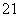 +x
+x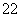 +x
+x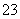 +x
+x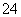 -16),则数据x1+2,x2+2,x3+2,x4+2的平均数为( )
-16),则数据x1+2,x2+2,x3+2,x4+2的平均数为( )
 D.无法求解
D.无法求解