函数f(x)在定义域R内可导,若f(x)=f(2﹣x),且(x﹣1)f′(x)>0,若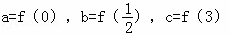 ,则a,b,c的大小关系是( )
,则a,b,c的大小关系是( )
|
| A. | a>b>c | B. | c>a>b | C. | b>a>c | D. | c>b>a |
设△ABC的三边长分别为a、b、c,△ABC的面积为S,内切圆半径为r,则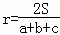 ,类比这个结论可知:四面体S﹣ABC的四个面的面积分别为S1、S2、S3、S4,内切球半径为r,四面体S﹣ABC的体积为V,则r=( )
,类比这个结论可知:四面体S﹣ABC的四个面的面积分别为S1、S2、S3、S4,内切球半径为r,四面体S﹣ABC的体积为V,则r=( )
|
| A. |
| B. |
|
|
| C. |
| D. |
|
Sn是数列{an}的前n项和,an= ,则S1=1﹣
,则S1=1﹣ ,S2=1﹣
,S2=1﹣ ,S3=1﹣
,S3=1﹣ ,S4=1﹣
,S4=1﹣ ,由此可以归纳出( )
,由此可以归纳出( )
|
| A. | Sn=1﹣ | B. | Sn=1﹣ | C. | Sn=1﹣ | D. | Sn=1﹣ |
演绎推理“因为对数函数y=logax(a>0且a≠1)是增函数,而函数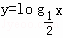 是对数函数,所以
是对数函数,所以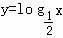 是增函数”所得结论错误的原因是( )
是增函数”所得结论错误的原因是( )
|
| A. | 大前提错误 | B. | 小前提错误 |
|
| C. | 推理形式错误 | D. | 大前提和小前提都错误 |
阅读程序框图,该程序运行后输出的k的值为( )

|
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
用反证法证明命题“:若 a,b∈N,ab能被3整除,那么a,b中至少有一个能被3整除”时,假设应为( )
|
| A. | a,b都能被3整除 | B. | a不能被3整除 |
|
| C. | a,b不都能被3整除 | D. | a,b都不能被3整除 |
已知p:x=2,q:0<x<3,则p是q的( )
|
| A. | 充分不必要条件 | B. | 必要不充分条件 |
|
| C. | 充要条件 | D. | 既不充分,又不必要条件 |
如图是集合的知识结构图,如果要加入“全集”,则应该放在( )

|
| A. | “集合的概念”的下位 | B. | “集合的表示”的下位 |
|
| C. | “基本关系”的下位 | D. | “基本运算”的下位 |
已知集合A={0,1,2},B={x|1<x<4},则A∩B=( )
|
| A. | {0} | B. | {1} | C. | {2} | D. | {1,2} |
 ﹣i(i是虚数单位),则z2= _________ .
﹣i(i是虚数单位),则z2= _________ .






