在平面直角坐标系中,定义d(P,Q)=|x1﹣x2|+|y1﹣y2|为两点P(x1,y1),Q(x2,y2)之间的“折线距离”,在这个定义下,给出下列命题:
①到原点的“折线距离”等于1的点的集合是一个圆;
②到原点的“折线距离”小于等于2的点构成的区域面积为8;
③到M(0,﹣2),N(0,2)两点的“折线距离”相等的点的轨迹方程是y=0;
④直线y=x+1上的点到N(0,2)的“折线距离”的最小值为1.
其中真命题有( )
|
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
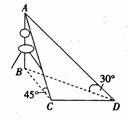
如图,要测量底部不能到达的某铁塔AB的高度,在塔的同一侧选择C、D两观测点,且在C、D两点测得塔顶的仰角分别为45°、30°.在水平面上测得∠BCD=120°,C、D两地相距600m,则铁塔AB的高度是( )
|
| A. | 120 | B. | 480m | C. | 240 | D. | 600m |
m、n是两条不同的直线,α、β、γ是三个不同的平面,则下列命题正确的是( )
|
| A. | 若α⊥β,α⊥γ,则β⊥γ | B. | 若m、n与α所成的角相等,则m∥n |
|
| C. | 若m⊥α,m∥β,则α⊥β | D. | 若m∥n,m⊂α,则n∥α |
已知数列{2n﹣(﹣1)n}的前10项和为( )
|
| A. | 210﹣3 | B. | 210﹣2 | C. | 211﹣3 | D. | 211﹣2 |
如图,一个空间几何体的正视图与侧视图都是边长为1的正三角形,俯视图为正方形,则其体积是( )

|
| A. |
| B. |
| C. |
| D. |
|
设x,y满足的约束条件是 ,则z=x+2y的最小值是( )
,则z=x+2y的最小值是( )
|
| A. | ﹣1 | B. | 3 | C. | 5 | D. | 6 |
数列{an}满足a1= ,an+1=1﹣
,an+1=1﹣ ,那么a10=( )
,那么a10=( )
|
| A. | ﹣1 | B. |
| C. | 1 | D. | 2 |
圆(x﹣3)2+y2=4与圆x2+(y﹣4)2=16的位置关系为( )
|
| A. | 内切 | B. | 外切 | C. | 相交 | D. | 相离 |
过点A(1,0)和点B(m,4)的直线与直线y=2x+1平行,则m等于( )
|
| A. | 3 | B. | 5 | C. | 7 | D. | 9 |
 m
m


