题目内容
在平面直角坐标系中,定义d(P,Q)=|x1﹣x2|+|y1﹣y2|为两点P(x1,y1),Q(x2,y2)之间的“折线距离”,在这个定义下,给出下列命题:
①到原点的“折线距离”等于1的点的集合是一个圆;
②到原点的“折线距离”小于等于2的点构成的区域面积为8;
③到M(0,﹣2),N(0,2)两点的“折线距离”相等的点的轨迹方程是y=0;
④直线y=x+1上的点到N(0,2)的“折线距离”的最小值为1.
其中真命题有( )
|
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
C

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
阅读程序框图,执行相应的程序,若输入x=4,则输出y的值为( )

|
| A. | ﹣ | B. | ﹣ | C. | ﹣ | D. | ﹣ |
已知变量x、y满足条件 ,则2x+y的最大值是( )
,则2x+y的最大值是( )
|
| A. | 3 | B. | 6 | C. | 9 | D. | 12 |
设x,y满足的约束条件是 ,则z=x+2y的最小值是( )
,则z=x+2y的最小值是( )
|
| A. | ﹣1 | B. | 3 | C. | 5 | D. | 6 |
已知集合A={0,1,2},B={x|1<x<4},则A∩B=( )
|
| A. | {0} | B. | {1} | C. | {2} | D. | {1,2} |
某同学在研究性学习中,收集到某制药厂车间工人数(单位:十人)与药品产量(单位:万盒)的数据如表所示:
| 工人数:x(单位:十人) | 1 | 2 | 3 | 4 |
| 药品产量:y(单位:万盒) | 3 | 4 | 5 | 6 |
(1)请画出如表数据的散点图;
(2)参考公式,根据表格提供的数据,用最小二乘法求出y关于x的线性回归方程y=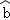 x+
x+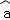 ;(参考数据
;(参考数据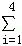 i2=30,
i2=30,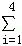 xiyi=50)
xiyi=50)
(3)试根据(2)求出的线性回归方程,预测该制药厂车间工人数为45时,药品产量是多少?




 (k∈R),对任意x∈[1,2],存在x0∈[﹣1,1],使得g(x)<f(x0)求k的取值范围.
(k∈R),对任意x∈[1,2],存在x0∈[﹣1,1],使得g(x)<f(x0)求k的取值范围.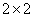 列联表:
列联表: 
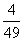 .
.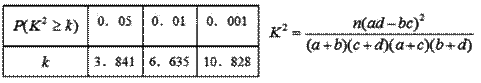 附:
附: