如图1，平面四边形ABCD关于直线AC对称，∠A=60°，∠C=
90°，CD=2，把△ABD沿BD折起（如图2），使二面角A-BD-C为直二面角．如图2，
（Ⅰ）求AD与平面ABC所成的角的余弦值；
（Ⅱ）求二面角B-AC-D的大小的正弦值．

给出下列命题：
①y=1是幂函数；
②函数f（x）=2^x-x²的零点有2个；
③(x+

1

x

+2)5展开式的项数是6项；
④函数y=sinx（x∈[-π，π]）图象与x轴围成的图形的面积是S=

∫

π -π

sinxdx；
⑤若ξ～N（1，σ²），且P（0≤ξ≤1）=0.3，则P（ξ≥2）=0.2；
其中真命题的序号是（写出所有正确命题的编号）．

已知O为坐标原点，向量

OA

=（1，sinα），

OB

=（0，cosα），

OC

=（2，-sinα），点P满足

AB

=

BP

．
（1）若O、P、C三点共线，求tanα的值；
（2）记函数f（α）=

PB

•

CA

，求函数f（α）的值域．

计算：cos²45°-sin²45°．

y=3sin2x的最大值为．

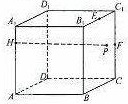
如图，已知正方体ABCD-A₁B₁C₁D₁的棱长为4，点H在棱AA₁上，且HA₁=1，点E、F分别为B₁C₁、CC₁的中点，P为侧面BCC₁B₁上一动点，且PE⊥PF，则当点P运动时，求HP²的最小值是（　　）

已知M（1，2），N（2，3），则线段MN的中点的坐标是．

已知抛物线C：y²=2px（p＞0）上横坐标为4的点到焦点的距离为5．
（1）求抛物线C的方程；
（2）设直线y=kx+b与抛物线C交于两点A（x₁，y₁），B（x₂，y₂），且|y₁-y₂|=a（a＞0，且a为常数）．过弦AB的中点M作平行于x轴的直线交抛物线于点D，连结AD、BD得到△ABD．
（Ⅰ）求证：a²k²=16（1-kb）；
（Ⅱ）求证：△ABD的面积为定值．

抛物线y²=2px上不同两点A，B（异于原点O）若OA，OB所在直线斜率之和定值m（m≠0）则直线AB必经过（　　）

已知椭圆

x2

a2

+

y2

b2

=1（a＞b＞0）的右焦点为F（3，0），过F的直线交椭圆与A，B两点，若AB的中点坐标为（1，-1），则a+b的值为．