10分)某公司在过去几年内使用某种型号的灯管1000支,该公司对这些灯管的使用寿命
(单位:小时)进行了统计,统计结果如下表所示:
| 分组 |  |  |  | 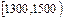 |  | 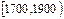 |  |
| 组数 | 48 | 121 | 208 | 223 | 193 | 165 | 42 |
| 频率 | | | | | | | |
(2) 根据上述统计结果,计算灯管使用寿命不足1500小时的频率;
(3) 该公司某办公室新安装了这种型号的灯管3支,若将上述频率作为概率,试求至少有2支灯管的使用寿命不足1500小时的概率
某车间为了规定工时定额,需要确定加个某零件所花费的时间,为此作了四次实验,得到的数据如下:
| 零件的个数x(个) | 2 | 3 | 4 | 5 |
| 加工的时间y(小时) | 2.5 | 3 | 4 | 4.5 |
(2) 试预测加工10个零件需要多少时间?

已知x与y之间的一组数据
| x | 0 | 1 | 2 | 3 |
| y | 1 | 3 | 5 | 7 |
(2)若
 x与y线性相关,写出线性回归方程必定经过的点
x与y线性相关,写出线性回归方程必定经过的点(3)若x与y线性相关求出线性回归方程,
(4)说出2个刻画回归效果的手段,假设R
 =0.74
=0.74 说明什么问题。
说明什么问题。参考公式
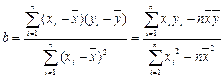
(本小题满分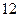 分)有甲、乙两个班,进行数学考试,按学生考试及格与不及格统计成绩后,得到如下的列联表
分)有甲、乙两个班,进行数学考试,按学生考试及格与不及格统计成绩后,得到如下的列联表
| | 不及格 | 及格 | 总计 |
| 甲班 | 10 | 35 | M |
| 乙班 | 7 | 38 | 45 |
| 总计 | 17 | 73 | N |
(2) 写出求k
 观测值的计算式
观测值的计算式(3) 假设k
 =0.6527你有多大把握认为成绩及格与班级
=0.6527你有多大把握认为成绩及格与班级 有关?
有关?k
 =7.121又说明什么?
=7.121又说明什么?(P(k

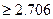 )
)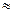 0.100,P(k
0.100,P(k
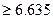 )
)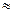 0.010)
0.010) (本小题12分)
已知某商品的价格 (元)与需求量
(元)与需求量 (件)之间的关系有如下一组数据:
(件)之间的关系有如下一组数据:
 | 14 | 16 | 18 | 20 | 22 |
 | 12 | 10 | 7 | 5 | 3 |
 关于
关于 的散点图
的散点图(2)用最小二乘法求出回归直线方程
(3)计算
 的值,并说明回归模型拟合程度的好坏。
的值,并说明回归模型拟合程度的好坏。 (本题满分12分)班主任为了对本班学生的考试成绩进行分析,决定从全班 位女同学,
位女同学, 位男同学中随机抽取一个容量为
位男同学中随机抽取一个容量为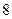 的样本进行分析。
的样本进行分析。
(Ⅰ)如果按性别比例分层抽样,可以得到多少个不同的样本(只要求写出算式即可,不必计算出结果);
(Ⅱ)随机抽取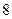 位同学,数学成绩由低到高依次为:
位同学,数学成绩由低到高依次为: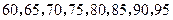 ;
;
物理成绩由低到高依次为: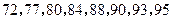 ,若规定
,若规定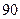 分(含
分(含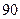 分)以
分)以 上为优秀,记
上为优秀,记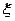 为这
为这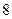 位同学中数学和物理分数均为优秀的人数,求
位同学中数学和物理分数均为优秀的人数,求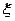 的分布列和数学期望;
的分布列和数学期望;
(Ⅲ)若这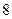 位同学的数学、物理分数事实上对应下表:
位同学的数学、物理分数事实上对应下表:
| 学生编号 | 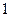 | 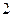 | 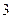 | 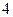 | 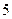 | 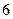 | 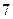 | 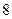 |
数学分数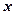 | 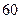 | 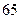 | 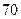 | 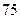 | 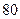 | 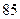 | 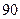 |  |
物理分数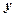 | 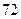 | 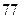 | 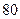 | 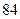 | 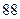 | 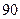 | 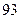 |  |
根据上表数据可知,变量
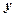 与
与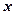
 之间具有较强的线性相关关系,求出
之间具有较强的线性相关关系,求出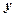 与
与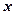 的线性回归方程(系数精确到
的线性回归方程(系数精确到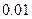 ).(参考公式:
).(参考公式: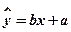 ,其中
,其中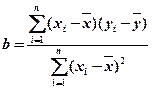 ,
,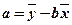 ; 参考数据:
; 参考数据: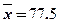 ,
,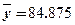 ,
,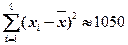 ,
, ,
,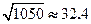 ,
,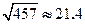 ,
,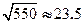 )
)  组,第一组
组,第一组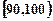 、第二组
、第二组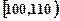 …第六组
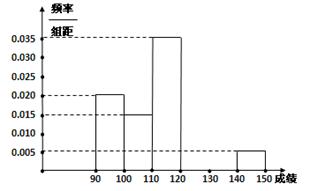
…第六组 . 如图为其频率分布直方图的一部分,若第四、五、六组的人数依次成等差数列,且第六组有4人.
. 如图为其频率分布直方图的一部分,若第四、五、六组的人数依次成等差数列,且第六组有4人.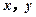 . 若
. 若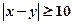 ,则称此二
,则称此二 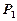 ;
;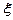 分布列及期望
分布列及期望 .
.
 查中,共调查了124人,其中女性70人,男性54人。女性中有43人的休闲方式是看电视,27人的休闲方式是参加体育运动。男性中有21人的休闲方式是看电视,33人的休闲方式是参加体育运动。
查中,共调查了124人,其中女性70人,男性54人。女性中有43人的休闲方式是看电视,27人的休闲方式是参加体育运动。男性中有21人的休闲方式是看电视,33人的休闲方式是参加体育运动。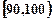 、第二组
、第二组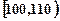 …第六组
…第六组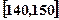 . 如图为其频率分布直方图的一部分,若第四、五、六组的人数依次成等差数列,且第六组有4人.
. 如图为其频率分布直方图的一部分,若第四、五、六组的人数依次成等差数列,且第六组有4人.
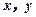 . 若
. 若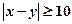 ,则称此二人为“黄金帮扶组”,试求选出的二人为“黄金帮扶组”的概率
,则称此二人为“黄金帮扶组”,试求选出的二人为“黄金帮扶组”的概率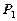 ;
;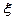 分布列及期望.
分布列及期望.