17.有甲乙两个班级进行数学考 试,按照大于等于85分为优秀,85分以下为非优秀统计成绩后,得到如下的列联表:
试,按照大于等于85分为优秀,85分以下为非优秀统计成绩后,得到如下的列联表:
| | 优秀 | 非优秀 | 总计 |
| 甲班 | 10[来源:学科网ZXXK] | | |
| 乙班 | | 30 | [来源:学#科#网] |
| 合计 | | | 105 |
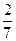
(1)请完成上面的列联表;
(2)根据列联表的数据,若按95%的可靠性要求,能否认为“成
 绩与班级有关系”。
绩与班级有关系”。(3)若按下面的方法从甲班优秀的学生抽取一人;把甲班优秀的10名学生从2到11进行编号,先后两次抛掷一枚均匀的骰子,出现的点数之和为被抽取的人的序号,试求抽到6或10的概率。
(本小题满分12分)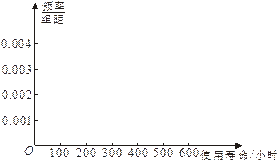
对某电子元件进行寿命追踪调查,情况如下:
| 寿命/小时 | 100~200 | 200~300 | 300~400 | 400~500 | 500~600 |
| 个数 | 20 | 30 | 80 | 40 | 30 |
| 分组 | 频数 | 频率 |
| 100~200 | | |
| 200~300 | | |
| 300~400 | | |
| 400~500 | | |
| 500~600 | | |
| 合计 | | |
(3)估计电子元件寿命在100~400小时以内的频率;
(本小题满分12分)
某兴趣小组欲研究昼夜温差大小与患感冒人数多少之间的关系,他们分别到气象局与某医院抄录了1至6月份每月10号的昼夜温差情况与因患感冒而就诊的人数,得到如下资料:
| 日 期 | 1月10日 | 2月10日 | 3月10日 | 4月10日 | 5月10日 | 6月10日 |
昼夜温差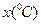 | 10 | 11 | 13 | 12 | 8 | 6 |
就诊人数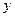 个 个 | 22 | 25 | 29 | 26 | 16 | 12 |
⑴求选取的2组数据恰好是相邻两个月的概率;
⑵若选取的是1月与6月的两组数据,请根据2至5月份的数据,求出
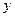 关于
关于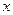 的线性回归方程
的线性回归方程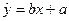 ;
;⑶若由线性回归方程得到的估计数据与所选出的检验数据的误差均不超过2人,则认为得到的线性回归方程是理想的,试问该小组所得线性www.ks5u.com回归方程是否理想?
 分配相应的低息贷款金额,其评估标准和贷款金额如下表:
分配相应的低息贷款金额,其评估标准和贷款金额如下表: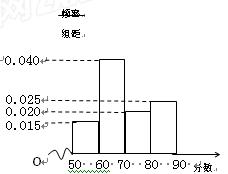
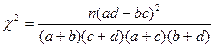
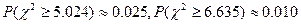 )
) 意
意