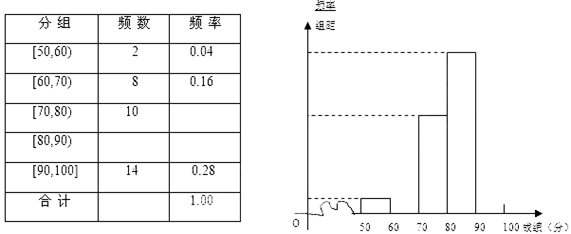
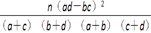某市为节约用水,计划在本市试行居民生活用水定额管理,为了较为合理地确定居民日常用水量的标准,通过抽样获得了100位居民某年的月均用水量(单位:吨),右表是100位居民月均用水量的频率分布表,根据右表解答下列问题:
| 分组 | 频数 | 频率 |
| [0,1) | 10 | 0.10 |
| [1,2) |  | 0.20 |
| [2,3) | 30 | 0.30 |
| [3,4) | 20 | 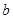 |
| [4,5) | 10 | 0.10 |
| [5,6] | 10 | 0.10 |
| 合计 | 100 | 1.00 |

(1)求右表中
 和
和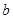 的值;
的值;(2)请将频率分布直方图补充完整,并根据直方图估计该市每位居民月均用水量的众数.
对400个某种型号的电子元件进行寿命追踪调查,其频率分布表如下表:
| 寿命(h) | 频率 |
| 500600 | 0.10 |
| 600700 | 0.15 |
| 700800 | 0.40 |
| 800900 | 0.20 |
| 9001000 | 0.15 |
| 合计 | 1 |
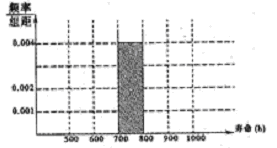
(I)在下图中补齐频率分布直方图;
(II)估计元件寿命在500800h以内的概率。
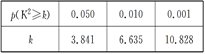
有甲、乙两个班级进行数学考试,按照大于或等于85分为优秀,85分以下为非优秀统计成绩后,得到如下的 列联表:已知从全部210人中随机抽取1人为优秀的概率为
列联表:已知从全部210人中随机抽取1人为优秀的概率为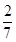 .
.
| | 优秀 | 非优秀 | 总计 |
| 甲班 | 20 | | |
| 乙班 | | 60 | |
| 合计 | | | 210 |
(Ⅰ)请完成上面的
 列联表,并判断若按99%的可靠性要求,能否认为“成绩与班级有关”;
列联表,并判断若按99%的可靠性要求,能否认为“成绩与班级有关”;(Ⅱ)从全部210人中有放回抽取3次,每次抽取1人,记被抽取的3人中的优秀人数为
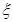 ,若每次抽取的结果是相互独立的,求
,若每次抽取的结果是相互独立的,求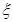 的分布列及数学期望
的分布列及数学期望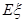 .
.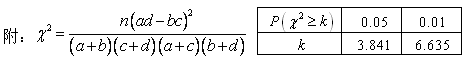
一台机器使用的时间较长,但还可以使用,它按不同的转速生产出来的某机械零件有一些会有缺点,每小时生产有缺点零件的多少,随机器的运转的速度而变化,下表为抽样试验的结果:
| 转速x(转/秒) | 16 | 14 | 12 | 8 |
| 每小时生产有缺点的零件数y(件) | 11 | 9 | 8 | 5 |
画出散点图,并通过散点图确定变量y对x是否线性相关;
(2)如果y对x有线性相关关系,求回归直线方程;
(3)若实际生产中,允许每小时的产品中有缺点的零件最多为10个,那么机器的运转速度应控制在什么范围内?(精确到0.0001)
“中国式过马路”存在很大的交通安全隐患.某调查机构为了解路人对“中国式过马路 ”的态度是否与性别有关,从马路旁随机抽取30名路人进行了问卷调查,得到了如下列联表:
| | 男性 | 女性 | 合计 |
| 反感 | 10 | | |
| 不反感 | | 8 | |
| 合计 | | | 30 |
已知在这30人中随机抽取1人抽到反感“中国式过马路 ”的路人的概率是
 .
.(Ⅰ)请将上面的列表补充完整(在答题卡上直接填写结果,不需要写求解过程),并据此资料分析反感“中国式过马路 ”与性别是否有关?(

当
 <2.706时,没有充分的证据判定变量性别有关,当
<2.706时,没有充分的证据判定变量性别有关,当
 >2.706时,有90%的把握判定变量性别有关,当
>2.706时,有90%的把握判定变量性别有关,当 >3.841时,有95%的把握判定变量性别有关,当
>3.841时,有95%的把握判定变量性别有关,当
 >6.635时,有99%的把握判定变量性别有关)
>6.635时,有99%的把握判定变量性别有关)(Ⅱ)若从这30人中的女性路人中随机抽取2人参加一活动,记反感“中国式过马路”的人数为X,求X的分布列和数学期望.
“中国式过马路”存在很大的交通安全隐患.某调查机构为了解路人对“中国式过马路 ”的态度是否与性别有关,从马路旁随机抽取30名路人进行了问卷调查,得到了如下列联表:
| | 男性 | 女性 | 合计 |
| 反感 | 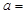 10 10 | 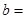 | |
| 不反感 | 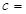 |  8 8 | |
| 合计 | | | 30 |
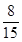 .
.(Ⅰ)请将上面的2×2列联表补充完整(在答题卡上直接填写结果,不需要写求解过程),并据此资料分析反感“中国式过马路 ”与性别是否有关?
(Ⅱ)若从这30人中的女性路人中随机抽取2人参加一活动,记反感“中国式过马路”的人数为X,求X的分布列和数学期望.
参考数据和公式:
2×2列联表
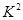 公式:
公式: ,
,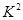 的临界值表:
的临界值表: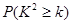 | 0.50 | 0.40 | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
 | 0.455 | 0.708 | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
 段的有多少人;
段的有多少人; 与身高
与身高 进行测量,得到数据(单位均为
进行测量,得到数据(单位均为 )作为样本如下表所示.
)作为样本如下表所示.
 ;
; ,试估计此人的身高;
,试估计此人的身高; ,
, ,
, ,
, )
)