题目内容
中日“钓鱼岛争端”问题越来越引起社会关注,我校对高一600名学生进行了一次“钓鱼岛”知识测试,并从中抽取了部分学生的成绩(满分100分)作为样本,绘制了下面尚未完成的频率分布表和频率分布直方图.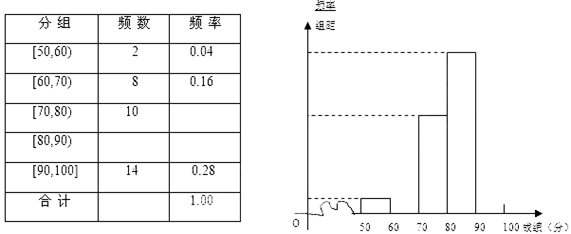
(1)填写答题卡频率分布表中的空格,补全频率分布直方图,并标出每个小矩形对应的纵轴数据;
(2)试估计该年段成绩在 段的有多少人;
段的有多少人;
(3)请你估算该年级的平均分.
(1)

(2)312
(3)81.4
解析试题分析:(1)频数一列应为:16 50 频率一列为:0.2 0.32
纵轴数据为:0.004 0.016 0.020 0.028 0.032
(2) 在50人中,在 的频率为
的频率为 由此可以估计年级段在
由此可以估计年级段在 的人数有
的人数有
(3) 设所求平均数为 ,由频率分布直方图可得:
,由频率分布直方图可得:
所以该年级段的平均分数约为81.4分
考点:频数、频率和样本容量
点评:频数、频率和样本容量三者之间的关系是知二求一,这种问题会出现在选择和填空中,有的省份也会以大题的形式出现,把它融于统计问题中.

 名校课堂系列答案
名校课堂系列答案某种产品的广告费支出 与销售额
与销售额 (单位:万元)之间有如下对应数据:
(单位:万元)之间有如下对应数据:
 | 2 | 4 | 5 | 6 | 8 |
 | 30 | 40 | 60 | 50 | 70 |
(Ⅱ)试预测广告费支出为10万元时,销售额多大?
(Ⅲ)在已有的五组数据中任意抽取两组,求至少有一组数据其预测值与实际值之差的绝对值不超过5的概率。
(参考数据:

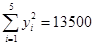
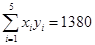 ,
,参考公式:回归直线方程
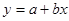 ,其中
,其中 )
) 有甲、乙两个班级进行数学考试,按照大于或等于85分为优秀,85分以下为非优秀统计成绩后,得到如下的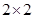 列联表:已知从全部210人中随机抽取1人为优秀的概率为
列联表:已知从全部210人中随机抽取1人为优秀的概率为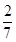 .
.
| | 优秀 | 非优秀 | 总计 |
| 甲班 | 20 | | |
| 乙班 | | 60 | |
| 合计 | | | 210 |
(Ⅰ)请完成上面的
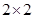 列联表,并判断若按99%的可靠性要求,能否认为“成绩与班级有关”;
列联表,并判断若按99%的可靠性要求,能否认为“成绩与班级有关”;(Ⅱ)从全部210人中有放回抽取3次,每次抽取1人,记被抽取的3人中的优秀人数为
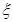 ,若每次抽取的结果是相互独立的,求
,若每次抽取的结果是相互独立的,求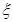 的分布列及数学期望
的分布列及数学期望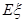 .
.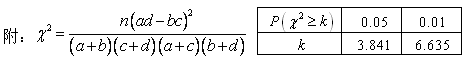
在生产过程中,测得纤维产品的纤度(表示纤维粗细的一种量)共有100个数据,将数据分组如表:
| 分组 | 频数 |
 | 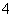 |
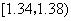 |  |
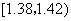 |  |
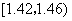 | 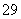 |
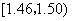 |  |
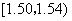 |  |
| 合计 |  |
(2)估计纤度落在
 中的概率及纤度小于
中的概率及纤度小于 的概率是多少?
的概率是多少?(3)从频率分布直方图估计出纤度的众数、中位数和平均数.
为了解目前老年人居家养老还是在敬老院养老的意向,共调查了50名老年人,其中男性明确表示去敬老院养老的有5人,女性明确表示居家养老的有10人,已知在全部50人中随机地抽取1人明确表示居家养老的概率为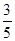 。
。
(1)请根据上述数据建立一个2×2列联表;(2)居家养老是否与性别有关?请说明理由。
参考数据:
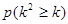 | 0.100 | 0.050 | 0.025 | 0.010 | 0.001 |
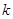 | 2.706 | 3.841 | 5.024 | 6.635 | 10.828 |
在某次测验中,有6位同学的平均成绩为75分.用xn表示编号为n(n=1,2, ,6)的同学所得成绩,且前5位同学的成绩如下:
| 编号n | 1 | 2 | 3 | 4 | 5 |
| 成绩xn | 70 | 76 | 72 | 70 | 72 |
(2)从前5位同学中,随机地选2位同学,求恰有1位同学成绩在区间(68,75)中的概率.

 ℃为低热,
℃为低热, ℃为中等热,
℃为中等热, ℃为高热。按此规定,记事件A为“从甲班发热的同学中任选两人,有中等热的同学”,记事件B为“从乙班发热的同学中任选两人,有中等热的同学”,分别求事件A和事件B的概率.
℃为高热。按此规定,记事件A为“从甲班发热的同学中任选两人,有中等热的同学”,记事件B为“从乙班发热的同学中任选两人,有中等热的同学”,分别求事件A和事件B的概率. 只,给每只鱼做上不影响其存活的标记,然后放回池塘,待完全混合后,再每次从池塘中随机的捕出
只,给每只鱼做上不影响其存活的标记,然后放回池塘,待完全混合后,再每次从池塘中随机的捕出 次,并将记录获取的数据做成以下的茎叶图。
次,并将记录获取的数据做成以下的茎叶图。

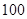 条鱼进行称重,据称重鱼的重量介于
条鱼进行称重,据称重鱼的重量介于 (单位:千克)之间,将测量结果按如下方式分成九组:第一组
(单位:千克)之间,将测量结果按如下方式分成九组:第一组 、第二组
、第二组 ;……,第九组
;……,第九组 。右图是按上述分组方法得到的频率分布直方图的一部分。
。右图是按上述分组方法得到的频率分布直方图的一部分。 千克以上(含
千克以上(含 的等差数列,请将频率分布直方图补充完整;
的等差数列,请将频率分布直方图补充完整; 只鱼中出现鲤鱼的次数为
只鱼中出现鲤鱼的次数为 ,求
,求 的住户属于“低碳族”,则称这个小区为“低碳小区”,否则称为“非低碳小区”.已知备选的5个居民小区中有三个非低碳小区,两个低碳小区.
的住户属于“低碳族”,则称这个小区为“低碳小区”,否则称为“非低碳小区”.已知备选的5个居民小区中有三个非低碳小区,两个低碳小区.
 ,调查显示其“低碳族”的比例为
,调查显示其“低碳族”的比例为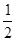 ,数据如图1所示,经过同学们的大力宣传,三个月后,又进行了一次调查,数据如图2所示,问这时小区
,数据如图1所示,经过同学们的大力宣传,三个月后,又进行了一次调查,数据如图2所示,问这时小区