某工厂有25周岁以上(含25周岁)工人300名,25周岁以下工人200名.为研究工人的日平均生产量是否与年龄有关,现采用分层抽样的方法,从中抽取了100名工人,先统计了他们某月的日平均生产件数,然后按工人年龄在“25周岁以上(含25周岁)”和“25周岁以下”分为两组,再将两组工人的日平均生产件数分为5组: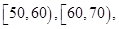
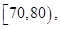
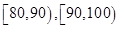 分别加以统计,得到如图所示的频率分布直方图.
分别加以统计,得到如图所示的频率分布直方图.
(I)从样本中日平均生产件数不足60件的工人中随机抽取2人,求至少抽到一名“25周岁以下组”工人的概率;
(II)规定日平均生产件数不少于80件者为“生产能手”,请你根据已知条件完成列联表,并判断是否有90%的把握认为“生产能手与工人所在的年龄组有关”?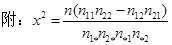
 | 0.100 | 0.050 | 0.010 | 0.001 |
| k | 2.706 | 3.841 | 6.635 | 10.828 |
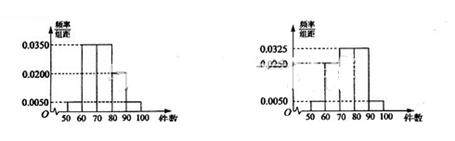
25周岁以上组 25周岁以下组
给出施化肥量(kg)对水稻产量(kg)影响的试验数据:
| 施化肥量x | 15 | 20 | 25 | 30 |
| 水稻产量y | 330 | 345 | 365 | 405 |
(2)请估计当施化肥量为10时,水稻产量为多少?
(已知:7.5×31.25+2.5×16.25+2.5×3.75+7.5×43.75=612.5,2×7.5×7.5+2×2.5×2.5=125)
某服装商场为了了解毛衣的月销售量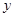 (件)与月平均气温
(件)与月平均气温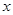 (℃)之间的关系,随机统计了某4个月的月销售量与当月平均气温,其数据如下表:
(℃)之间的关系,随机统计了某4个月的月销售量与当月平均气温,其数据如下表:
月平均气温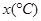 | 17 | 13 | 8 | 2 |
月销售量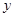 (件) (件) | 24 | 33 | 40 | 55 |
(2) 求线性回归方程
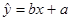 ;
;(3)气象部门预测下个月的平均气温约为6ºC,据此估计该商场下个月毛衣的销售量.(
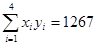 ,
,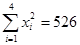 )
) 某初级中学共有学生2000名,各年级男、女生人数如下表:
| | 初一年级 | 初二年级 | 初三年级 |
| 女生 | 373 | 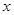 | 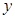 |
| 男生 | 377 | 370 | 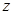 |
(1)求
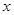 的值;
的值;(2)现用分层抽样的方法在全校抽取48名学生,问应在初三年级抽取多少名?
以下是某地搜集到的新房屋的销售价格y和房屋的面积x的数据:
| 房屋面积(m2) | 115 | 110 | 80 | 135 | 105 |
| 销售价格(万元) | 24.8 | 21.6 | 18.4 | 29.2 | 22 |
(2)求线性回归方程,并在散点图中加上回归直线;
(3)根据(2)的结果估计当房屋面积为150 m2时的销售价格.


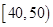 ,
,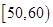 ,
, 后得到如图的频率分布直方图.
后得到如图的频率分布直方图.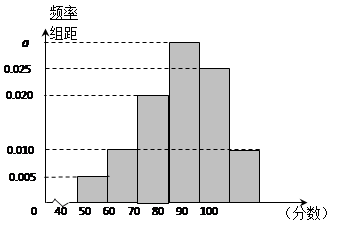
 的值;
的值; ,
, )
) 只,给每只鱼做上不影响其存活的标记,然后放回池塘,待完全混合后,再每次从池塘中随机的捕出
只,给每只鱼做上不影响其存活的标记,然后放回池塘,待完全混合后,再每次从池塘中随机的捕出 次,并将记录获取的数据做成以下的茎叶图。
次,并将记录获取的数据做成以下的茎叶图。

 条鱼进行称重,据称重鱼的重量介于
条鱼进行称重,据称重鱼的重量介于 (单位:千克)之间,将测量结果按如下方式分成九组:第一组
(单位:千克)之间,将测量结果按如下方式分成九组:第一组 、第二组
、第二组 ;……,第九组
;……,第九组 。右图是按上述分组方法得到的频率分布直方图的一部分。
。右图是按上述分组方法得到的频率分布直方图的一部分。 千克以上(含
千克以上(含 的等差数列,请将频率分布直方图补充完整;
的等差数列,请将频率分布直方图补充完整; 只鱼中出现鲤鱼的次数为
只鱼中出现鲤鱼的次数为 ,求
,求