题目内容
某校从高一年级学生中随机抽取40名学生作为样本,将他们的期中考试数学成绩(满分100分,成绩均为不低于40分的整数)分成六组: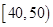 ,
,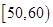 ,
,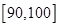 后得到如图的频率分布直方图.
后得到如图的频率分布直方图.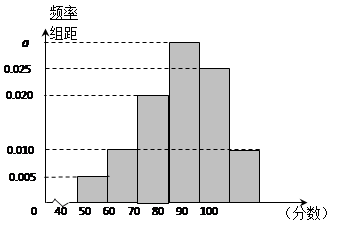
(Ⅰ)求图中实数 的值;
的值;
(Ⅱ)若该校高一年级共有学生500人,试估计该校高一年级在考试中成绩不低于60分的人数;
(Ⅲ)若从样本中数学成绩在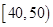 与
与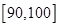 两个分数段内的学生中随机选取两名学生,试用列举法求这两名学生的数学成绩之差的绝对值不大于10的概率.
两个分数段内的学生中随机选取两名学生,试用列举法求这两名学生的数学成绩之差的绝对值不大于10的概率.
(1)0.03
(2)425
(3)
解析试题分析:解:(Ⅰ)由
可得 2分
2分
(Ⅱ)数学成绩不低于60分的概率为: 4分
4分
数学成绩不低于60分的人数为 人 5分
人 5分
(Ⅲ)数学成绩在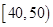 的学生人数:
的学生人数: 人 6分
人 6分
数学成绩在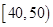 的学生人数:
的学生人数: 人 7分
人 7分
设数学成绩在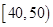 的学生为
的学生为 ,
,
数学成绩在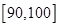 的学生为
的学生为 8分
8分
两名学生的结果为: ,
,
 共
共 种 10分
种 10分
其中两名学生的数学成绩之差的绝对值不大于10的情况有 ,
, ,
, ,
, ,
, ,
, ,
, 共7种, 12分
共7种, 12分
因此,抽取的两名学生的数学成绩之差的绝对值不大于10的概率为 13分
13分
考点:直方图以及古典概型
点评:主要是考查了直方图以及古典概型概率的计算,属于基础题。

某校高三有甲、乙两个班,在某次数学测试中,每班各抽取5份试卷,所抽取的平均得分相等(测试满分为100分),成绩统计用茎叶图表示如下:
| 甲 | | 乙 |
| 9 8 | 8 | 4 8 9 |
| 2 1 0 | 9 |  6 6 |
(1)求
 ;
;(2)学校从甲班的5份试卷中任取两份作进一步分析,在抽取的两份样品中,求至多有一份得分在
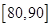 之间的概率.
之间的概率. 某高中在校学生2000人,高一年级与高二年级人数相同并且都比高三年级多1人,为了响应市教育局“阳光体育”号召,该校开展了跑步和跳绳两项比赛,要求每人都参加而且只参加其中一项,各年级参与项目人数情况如下表:
| | 高一年级 | 高二年级 | 高三年级 |
| 跑步 |  | 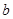 | 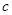 |
| 跳绳 |  |  | 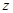 |
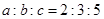 ,全校参与跳绳的人数占总人数的
,全校参与跳绳的人数占总人数的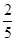 ,为了了解学生对本次活动的满意度,采用分层抽样从中抽取一个200人的样本进行调查,则高二年级中参与跑步的同学应抽取 人.
,为了了解学生对本次活动的满意度,采用分层抽样从中抽取一个200人的样本进行调查,则高二年级中参与跑步的同学应抽取 人. 某服装商场为了了解毛衣的月销售量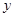 (件)与月平均气温
(件)与月平均气温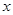 (℃)之间的关系,随机统计了某4个月的月销售量与当月平均气温,其数据如下表:
(℃)之间的关系,随机统计了某4个月的月销售量与当月平均气温,其数据如下表:
月平均气温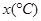 | 17 | 13 | 8 | 2 |
月销售量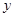 (件) (件) | 24 | 33 | 40 | 55 |
(2) 求线性回归方程
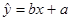 ;
;(3)气象部门预测下个月的平均气温约为6ºC,据此估计该商场下个月毛衣的销售量.(
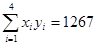 ,
,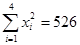 )
) 为了解某班学生喜爱打篮球是否与性别有关,对本班50人进行了问卷调查得到了如下的列联表:
| | 喜爱打篮球 | 不喜爱打篮球 | 合计 |
| 男生 | | 5 | |
| 女生 | 10 | | |
| 合计 | | | 50 |
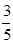 .
.(1)请将上面的列联表补充完整;
(2)是否在犯错误的概率不超过0.5%的前提下认为喜爱打篮球与性别有关?说明你的理由.下面的临界值表供参考:
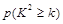 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005] | 0.001 |
 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
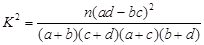 ,其中
,其中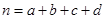 )
)
通过随机询问某校110名高中学生在购买食物时是否看营养说明,得到如下的列联表:
性别与看营养说明列联表 单位: 名
| | 男 | 女 | 总计 |
| 看营养说明 | 50 | 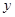 | 80 |
| 不看营养说明 |  | 20 | 30 |
| 总计 | 60 | 50 | 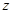 |
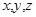 的值.
的值.(2)根据以上列联表,问有多大把握认为“性别与在购买食物时看营养说明”有关?
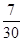 求:
求:
 是月用水量为[0,2)的家庭代表.
是月用水量为[0,2)的家庭代表. 是月用水量为[2,4]的家庭代表.若从这五位代表中任选两人参加水价听证会,请列举出所有不同的选法,并求家庭代表
是月用水量为[2,4]的家庭代表.若从这五位代表中任选两人参加水价听证会,请列举出所有不同的选法,并求家庭代表