为了解某班关注NBA是否与性别有关,对本班48人进行了问卷调查得到如下的列联表:
| | 关注NBA | 不关注NBA | 合计 |
| 男生 | | 6 | |
| 女生 | 10 | | |
| 合计 | | | 48 |
 .
.(1)请将上面的表补充完整(不用写计算过程),并判断是否有95%的把握认为关注NBA与性别有关?说明你的理由.
(2)现记不关注NBA的6名男生中某两人为a,b,关注NBA的10名女生中某3人为c,d,e,从这5人中选取2人进行调查,求:至少有一人不关注NBA的被选取的概率。
下面的临界值表,供参考
| P(K2≥k) | 0.10 | 0.05 | 0.010 | 0.005 |
| K | 2.706 | 3.841 | 60635 | 7.879 |
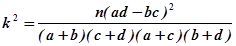 )其中n=a+b+c+d
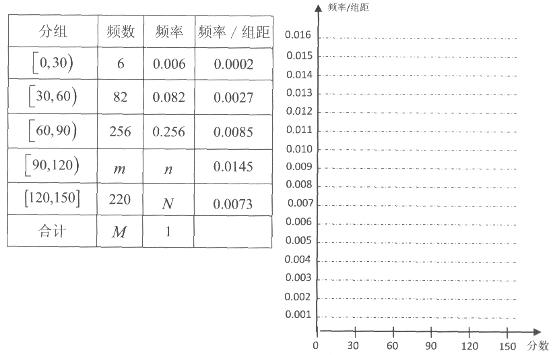
)其中n=a+b+c+d 某高校在2013年的自主招生考试成绩中随机抽取100名学生的笔试成绩,按成绩分组,得到的频率分布表如图所示.
| 组号 | 分组 | 频数 | 频率 |
| 第1组 |  | 5 | 0.050 |
| 第2组 | 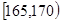 | ① | 0.350 |
| 第3组 |  | 30 | ② |
| 第4组 | 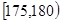 | 20 | 0.200 |
| 第5组 | 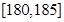 | 10 | 0.100 |
| 合计 | 100 | 1.00 | |
(1)请先求出频率分布表中①、②位置相应的数据,再在答题卷上完成下列频率分布直方图;

(2)为了能选拔出最优秀的学生,高校决定在笔试成绩高的第3、4、5组中用分层抽样抽取6名学生进入第二轮面试,求第3、4、5组每组各抽取多少名学生进入第二轮面试?
(3)在(2)的前提下,学校决定在6名学生中随机抽取2名学生接受A考官进行面试,求:第4组至少有一名学生被考官A面试的概率?
对甲、乙两名自行车赛手在相同条件下进行了6次测试,测得他们的最大速度(m/s)的数据如下表.
| 甲 | 27 | 38 | 30 | 37 | 35 | 31 |
| 乙 | 33 | 29 | 38 | 34 | 28 | 36 |
(2)分别求出甲、乙两名自行车赛手最大速度(m/s)数据的平均数、中位数、方差,并判断选谁参加比赛更合适.
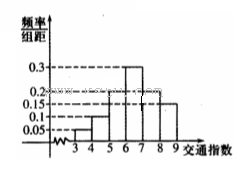
空气质量已成为城市居住环境的一项重要指标,空气质量的好坏由空气质量指数确定。空气质量指数越高,代表空气污染越严重:
| 空气质量指数 | 0~35 | 35~75 | 75~115 | 115~150 | 150~250 | ≥250 |
| 空气质量类别 | 优 | 良 | 轻度污染 | 中度污染 | 重度污染 | 严重污染 |

(1)估计某市一个月内空气受到污染的概率(规定:空气质量指数大于或等于75,空气受到污染);
(2)在空气质量类别为“良”、“轻度污染”、“中度污染”的监测数据中用分层抽样方法抽取一个容量为6的样本,若在这6数据中任取2个数据,求这2个数据所对应的空气质量类别不都是轻度污染的概率.

 名学生被考官L面试,求
名学生被考官L面试,求 的人群随机抽取
的人群随机抽取 人进行了一次生活习惯是否符合低碳观念的调查,若生活习惯符合低碳观念的称为“低碳族”,否则称为“非低碳族”,得到如下统计表和各年龄段人数频率分布直方图:
人进行了一次生活习惯是否符合低碳观念的调查,若生活习惯符合低碳观念的称为“低碳族”,否则称为“非低碳族”,得到如下统计表和各年龄段人数频率分布直方图:

 的值;
的值; 的“低碳族”中采用分层抽样法抽取6人参加户外低碳体验活动,其中选取2人作为领队,求选取的2名领队中恰有1人年龄在
的“低碳族”中采用分层抽样法抽取6人参加户外低碳体验活动,其中选取2人作为领队,求选取的2名领队中恰有1人年龄在 的概率.
的概率.