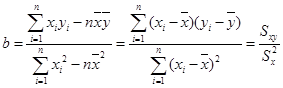为了了解高一年级学生的身高情况,某校按10%的比例对全校800名高一年级学生按性别进行抽样检查,得到如下频数分布表:
表1:男生身高频数分布表
| 身高(cm) | [160,165) | [165,170) | [170,175) | [175,180) | [180,185) | [185,190] |
| 频数 | 2 | 5 | 14 | 13 | 4 | 2 |
表2:男生身高频数分布表
| 身高(cm) | [150,155) | [150,160) | [160,165) | [165,170) | [170,175) | [175,180] |
| 频数 | 2 | 12 | 16 | 6 | 3 | 1 |
(1)分别估计高一年级男生和女生的平均身高;
(2)在样本中,从身高180cm以上的男生中任选2人,求至少有一人身高在185cm以上的概率.
为调查民营企业的经营状况,某统计机构用分层抽样的方法从A、B、C三个城市中,抽取若干个民营企业组成样本进行深入研究,有关数据见下表:(单位:个)
| 城市 | 民营企业数量 | 抽取数量 |
| A |  | 4 |
| B | 28 |  |
| C | 84 | 6 |
(1)求
 、
、 的值;
的值;(2)若从城市A与B抽取的民营企业中再随机选2个进行跟踪式调研,求这2个都来自城市A的概率.
下表是某市从3月份中随机抽取的 天空气质量指数(
天空气质量指数( )和“
)和“ ”(直径小于等于
”(直径小于等于 微米的颗粒物)
微米的颗粒物) 小时平均浓度的数据,空气质量指数(
小时平均浓度的数据,空气质量指数( )小于
)小于 表示空气质量优良.
表示空气质量优良.
| 日期编号 |  |  |  |  |  |  |  |  |  |  |
空气质量指数( ) ) |  |  |  |  |  |  |  |  |  |  |
“ ” ” 小时平均浓度( 小时平均浓度( ) ) |  |  |  |  |  |  |  |  |  |  |
(1)根据上表数据,估计该市当月某日空气质量优良的概率;
(2)在上表数据中,在表示空气质量优良的日期中,随机抽取两个对其当天的数据作进一步的分析,设事件
 为“抽取的两个日期中,当天‘
为“抽取的两个日期中,当天‘ ’的
’的 小时平均浓度不超过
小时平均浓度不超过 ”,求事件
”,求事件 发生的概率;
发生的概率;(3)在上表数据中,在表示空气质量优良的日期中,随机抽取
 天,记
天,记 为“
为“ ”
” 小时平均浓度不超过
小时平均浓度不超过 的天数,求
的天数,求 的分布列和数学期望.
的分布列和数学期望. 某学校餐厅新推出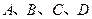 四款套餐,某一天四款套餐销售情况的条形图如下.为了了解同学对新推出的四款套餐的评价,对每位同学都进行了问卷调查,然后用分层抽样的方法从调查问卷中抽取20份进行统计,统计结果如下面表格所示:
四款套餐,某一天四款套餐销售情况的条形图如下.为了了解同学对新推出的四款套餐的评价,对每位同学都进行了问卷调查,然后用分层抽样的方法从调查问卷中抽取20份进行统计,统计结果如下面表格所示:
| | 满意 | 一般 | 不满意 |
| A套餐 | 50% | 25% | 25% |
| B套餐 | 80% | 0 | 20% |
| C套餐 | 50% | 50% | 0 |
| D套餐 | 40% | 20% | 40% |
(1)若同学甲选择的是A款套餐,求甲的调查问卷被选中的概率;
(2)若想从调查问卷被选中且填写不满意的同学中再选出2人进行面谈,求这两人中至少有一人选择的是D款套餐的概率.
某普通高中共有教师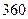 人,分为三个批次参加研修培训,在三个批次中男、女教师人数如下表所示:
人,分为三个批次参加研修培训,在三个批次中男、女教师人数如下表所示:
| | 第一批次 | 第二批次 | 第三批次 |
| 女教师 | 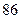 |  |  |
| 男教师 | 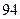 | 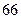 |  |
已知在全体教师中随机抽取1名,抽到第二、三批次中女教师的概率分别是
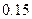 、
、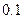 .
.(1)求
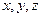 的值;
的值;(2)为了调查研修效果,现从三个批次中按
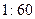 的比例抽取教师进行问卷调查,三个批次被选取的人数分别是多少?
的比例抽取教师进行问卷调查,三个批次被选取的人数分别是多少?(3)若从(2)中选取的教师中随机选出两名教师进行访谈,求参加访谈的两名教师“分别来自两个批次”的概率.
某种产品的广告费用支出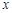 (万元)与销售额
(万元)与销售额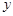 (万元)之间有如下的对应数据:
(万元)之间有如下的对应数据:
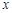 | 2 | 4 | 5 | 6 | 8 |
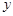 | 30 | 40 | 60 | 50 | 70 |
| x | 2 | 4 | 5 | 6 | 8 |
| y | 30 | 40 | 60 | 50 | 70 |
(1)画出散点图;
(2)求回归直线方程;
(3)据此估计广告费用为9万元时,销售收入
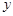 的值.
的值.参考公式:回归直线的方程
 ,其中
,其中 .
. 甲乙两个班级均为40人,进行一门考试后,按学生考试成绩及格与不及格进行统计,甲班及格人数为36人,乙班及格人数为24人.
(1)根据以上数据建立一个 的列联表;(2)试判断成绩与班级是否有关?
的列联表;(2)试判断成绩与班级是否有关?
参考公式: ;
;
| P(K2>k) | 0.50 | 0.40 | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k | 0.455 | 0.708 | 1.323 | 2.072 | 2.706 | 3.84 | 5.024 | 6.635 | 7.879 | 10.83 |

 名.以下茎叶图记录了该小组同学在一次数学测试中的成绩(单位:分).已知男生数据的中位数为
名.以下茎叶图记录了该小组同学在一次数学测试中的成绩(单位:分).已知男生数据的中位数为 ,女生数据的平均数为
,女生数据的平均数为 .
. ,
, 的值;
的值;
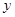 (万元)和房屋的面积
(万元)和房屋的面积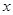 (
( )的数据 ,若由资料可知
)的数据 ,若由资料可知
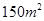 时的销售价格.
时的销售价格.