已知椭圆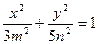 和双曲线
和双曲线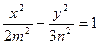 有公共的焦点,那么双曲线的渐近线方程是
有公共的焦点,那么双曲线的渐近线方程是  (
( )
)
A.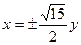 | B. | C. | D. |
下列曲线中离心率为 的是 ( )
的是 ( )
A.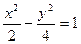 | B.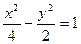 |
C.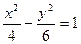 | D.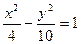 |
已知双曲线 的左、右焦点分别F1、F2,O为双曲线的中心,P
的左、右焦点分别F1、F2,O为双曲线的中心,P 是双曲线右支上的点,
是双曲线右支上的点, 的内切圆的圆心为I,且⊙I与x轴相切于点A,过F2作直线PI的垂线,垂足为B,若e为双曲线的率心率,则 ( )
的内切圆的圆心为I,且⊙I与x轴相切于点A,过F2作直线PI的垂线,垂足为B,若e为双曲线的率心率,则 ( )
A.|OB|=e| OA| OA| | B.|OA|="e|OB|" | C.|OB|="|OA|" | D.|OA|与|OB|关系不确定 |
一根竹竿长2米,竖直放在广场的水平地面上,在 时刻测得它的影长为4米,在
时刻测得它的影长为4米,在 时刻的影长为1米。这个广场上有一个球形物体,它在地面上的影子是椭
时刻的影长为1米。这个广场上有一个球形物体,它在地面上的影子是椭 圆,问在
圆,问在 、
、 这两个时刻该球形物体在地面上的两个椭圆影子的离心率之比为( )
这两个时刻该球形物体在地面上的两个椭圆影子的离心率之比为( )
| A.1:1 | B. :1 :1 | C. :1 :1 | D.2:1 |
若F(c, 0)是椭圆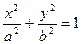 的右焦点,F与椭圆上点的距离的最大值为M,最小值为m,则椭圆上与F点的距离等于
的右焦点,F与椭圆上点的距离的最大值为M,最小值为m,则椭圆上与F点的距离等于 的点的坐标是( )
的点的坐标是( )
A.(c, ±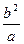 ) ) | B.(-c, ±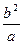 ) ) | C.(0, ±b) | D.不存在 |
设双曲线 的渐近线与抛物线
的渐近线与抛物线 有且只有两个公共点,则该双曲线的离心率
有且只有两个公共点,则该双曲线的离心率
| A.5 | B. | C. | D. |
抛物线 的准线方程是 ( )
的准线方程是 ( )
A. | B. | C. | D. |
F1、F2分别是椭圆 的左、右焦点,点P在椭圆上,线段PF2与
的左、右焦点,点P在椭圆上,线段PF2与 轴的交点为
轴的交点为
M,且 ,则点M到坐标原点O的距离是
,则点M到坐标原点O的距离是
A. | B.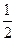 | C.1 | D.2 |
 、
、 、
、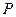 是双曲线
是双曲线 上不同的三点,且
上不同的三点,且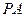 、
、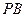 的斜率乘积
的斜率乘积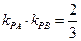 ,则该双曲线的离心率为( )
,则该双曲线的离心率为( ) 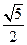 B.
B.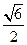 C.
C.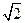 D.
D.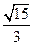
 分别为双曲线
分别为双曲线 的左、右焦点,若在双曲线右支上存在一点P,满足了
的左、右焦点,若在双曲线右支上存在一点P,满足了 ,且直线PF1与圆
,且直线PF1与圆
 相切,则该双曲线的渐近线方程为
相切,则该双曲线的渐近线方程为


