在极坐标系中,曲线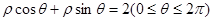 与
与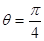 的交点的极坐标是( )
的交点的极坐标是( )
A.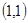 | B.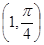 | C.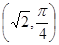 | D.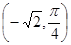 |
从抛物线y2 = 4x上一点P引抛物线准线的垂线,垂足为M,且|PM| = 5,设抛物线的焦点为F,则 的面积为( )
的面积为( )
| A.6 | B.8 | C.10 | D.15 |
若双曲线 -
- =1(a>0)的离心率为2,a= ( )
=1(a>0)的离心率为2,a= ( )
| A.2 | B. | C. | D.1 |
点 是曲线
是曲线 上的一个动点,曲线
上的一个动点,曲线 在点
在点 处的切线与
处的切线与 轴、
轴、 轴分别交于
轴分别交于 两点,点
两点,点 是坐标原点. 给出三个命题:①
是坐标原点. 给出三个命题:① ;②
;② 的周长有最小值
的周长有最小值 ;③曲线
;③曲线 上存在两点
上存在两点 ,使得
,使得 为等腰直角三角形.其中真命题的个数是
为等腰直角三角形.其中真命题的个数是
| A.1 | B.2 | C.3 | D.0 |
已知双曲线 的渐近线方程为
的渐近线方程为 ,则其离心率为( )
,则其离心率为( )
A. | B. | C. 或 或 | D. 或 或 |
双曲线 (
( )的两个焦点为
)的两个焦点为 ,若双曲线上存在一点
,若双曲线上存在一点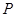 ,满足
,满足 ,则双曲线离心率的取值范围为
,则双曲线离心率的取值范围为
A. | B. | C. | D. |
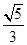
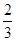
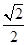
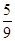
 的右支上一点,M、N分别是圆(x+5)2+y2=4和(x-5)2+y2=1上的点,则|PM|-|PN|的最大值为( )
的右支上一点,M、N分别是圆(x+5)2+y2=4和(x-5)2+y2=1上的点,则|PM|-|PN|的最大值为( ) 与双曲线C2:
与双曲线C2: 有公共的焦点,C2的一条渐近线与以C1的长轴为直径的圆相交于A、B两点,C1恰好将线段AB三等分,则( )
有公共的焦点,C2的一条渐近线与以C1的长轴为直径的圆相交于A、B两点,C1恰好将线段AB三等分,则( )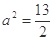 B.
B.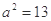 C.
C.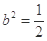 D.
D.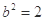
 ,左右焦点分别为
,左右焦点分别为 ,过
,过 的直线
的直线 交椭圆于
交椭圆于 两点,若
两点,若 的最大值为5,则
的最大值为5,则 的值是( )
的值是( )

