题目内容
点 是曲线
是曲线 上的一个动点,曲线
上的一个动点,曲线 在点
在点 处的切线与
处的切线与 轴、
轴、 轴分别交于
轴分别交于 两点,点
两点,点 是坐标原点. 给出三个命题:①
是坐标原点. 给出三个命题:① ;②
;② 的周长有最小值
的周长有最小值 ;③曲线
;③曲线 上存在两点
上存在两点 ,使得
,使得 为等腰直角三角形.其中真命题的个数是
为等腰直角三角形.其中真命题的个数是
| A.1 | B.2 | C.3 | D.0 |
C
解析

练习册系列答案
相关题目
已知点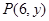 在抛物线
在抛物线 上,
上, 为抛物线焦点, 若
为抛物线焦点, 若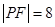 , 则点
, 则点 到抛物线准线的距离等于( )
到抛物线准线的距离等于( )
| A.2 | B.1 | C.4 | D.8 |
设定点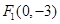 、
、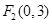 ,动点
,动点 满足条件
满足条件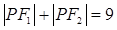 ,则点
,则点 的轨迹是( )
的轨迹是( )
| A.椭圆 | B.线段 | C.不存在 | D.线段或椭圆 |
已知双曲线 的左右焦点分别为
的左右焦点分别为 ,P为C的右支上一点,且
,P为C的右支上一点,且 =
= ,△
,△ 的面积等于( )
的面积等于( )
| A.24 | B.36 | C.48 | D.96 |
在极坐标系中,曲线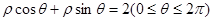 与
与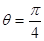 的交点的极坐标是( )
的交点的极坐标是( )
A.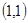 | B.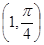 | C.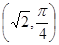 | D.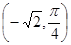 |
椭圆 与双曲线
与双曲线 有相同的焦点,则a的值是( )
有相同的焦点,则a的值是( )
A. | B.1或–2 | C.1或 | D.1 |
若抛物线的准线方程为x=–7, 则抛物线的标准方程为( )
| A.x2=–28y | B.y2=28x |
| C.y2=–28x | D.x2=28y |
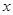 轴对称,它的顶点在坐标原点
轴对称,它的顶点在坐标原点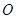 ,并且经过点
,并且经过点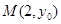 .若点
.若点 到该抛物线焦点的距离为
到该抛物线焦点的距离为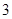 ,则
,则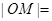 ( )
( )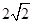
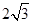

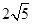
 =4:3:2,则曲线r的离心率等于
=4:3:2,则曲线r的离心率等于



