[2012·湖北高考]过点P(1,1)的直线,将圆形区域{(x,y)|x2+y2≤4}分成两部分,使得这两部分的面积之差最大,则该直线的方程为( )
| A.x+y-2=0 | B.y-1=0 |
| C.x-y=0 | D.x+3y-4=0 |
若圆O:x2+y2=4与圆C:x2+y2+4x-4y+4=0关于直线l对称,则直线l的方程是( )
| A.x+y=0 | B.x-y=0 |
| C.x-y+2=0 | D.x+y+2=0 |
设点 ,若在圆
,若在圆 上存在点
上存在点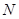 ,使得
,使得 ,则
,则 的取值范围是( )
的取值范围是( )
A. | B. | C. | D. |
若圆 与圆
与圆 ,则
,则 ( )
( )
| A.21 | B.19 | C.9 | D.-11 |
已知圆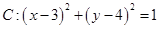 和两点
和两点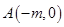 ,
,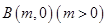 ,若圆
,若圆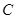 上存在点
上存在点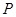 ,使得
,使得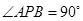 ,则
,则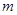 的最大值为( )
的最大值为( )
A. | B. | C.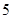 | D.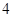 |
过点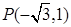 的直线
的直线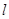 与圆
与圆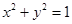 有公共点,则直线
有公共点,则直线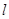 的倾斜角的取值范围是( )
的倾斜角的取值范围是( )
A.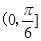 | B.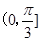 | C.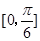 | D.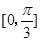 |
如图所示,AD,AE,BC分别与圆O切于点D,E,F,延长AF与圆O交于另一点G.给出下列三个结论: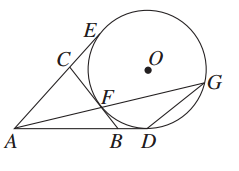
①AD+AE=AB+BC+CA;
②AF·AG=AD·AE;
③△AFB∽△ADG.
其中正确结论的序号是( )
| A.①② | B.②③ | C.①③ | D.①②③ |