题目内容
设点 ,若在圆
,若在圆 上存在点
上存在点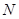 ,使得
,使得 ,则
,则 的取值范围是( )
的取值范围是( )
A. | B. | C. | D. |
A
解析试题分析:依题意,直线MN与圆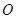 有公共点即可,即圆心
有公共点即可,即圆心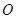 到直线MN的距离小于等于1即可,过
到直线MN的距离小于等于1即可,过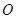 作
作
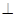 MN,垂足为A,在
MN,垂足为A,在 中,因为
中,因为
 ,故
,故
 ,所以
,所以 ,则
,则 ,解得
,解得 .
.
考点:1、解直角三角形;2、直线和圆的位置关系.

练习册系列答案
 同步练习河南大学出版社系列答案
同步练习河南大学出版社系列答案 同步练习西南大学出版社系列答案
同步练习西南大学出版社系列答案 补充习题江苏系列答案
补充习题江苏系列答案 学练快车道口算心算速算天天练系列答案
学练快车道口算心算速算天天练系列答案
相关题目
圆C:(x+1)2+(y-3)2=9上有两点P,Q关于直线x+my+4=0对称,则m等于( )
A.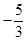 | B.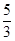 | C.-1 | D.1 |
设P是圆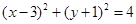 上的动点,Q是直线
上的动点,Q是直线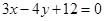 上的动点,则
上的动点,则 的最小值为( )
的最小值为( )
| A.1 | B.2 | C.3 | D.4 |
设圆的方程是x2+y2+2ax+2y+(a-1)2=0,若0<a<1,则原点与圆的位置关系是( )
| A.原点在圆上 | B.原点在圆外 |
| C.原点在圆内 | D.不确定 |
如图所示,AD,AE,BC分别与圆O切于点D,E,F,延长AF与圆O交于另一点G.给出下列三个结论: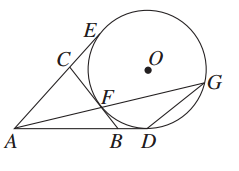
①AD+AE=AB+BC+CA;
②AF·AG=AD·AE;
③△AFB∽△ADG.
其中正确结论的序号是( )
| A.①② | B.②③ | C.①③ | D.①②③ |
若圆x2+y2-2kx+2y+2=0(k>0)与两坐标轴无公共点,那么实数k的取值范围为( )
| A.-1<k<1 | B.1<k<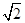 |
| C.1<k<2 | D.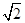 <k<2 <k<2 |
 中,点P到两点
中,点P到两点 ,
, 的距离之和等于4,设点P的轨迹为
的距离之和等于4,设点P的轨迹为 .
. 与C交于A,B两点.k为何值时
与C交于A,B两点.k为何值时

 ?此时
?此时 的值是多少?
的值是多少? 上,圆C过坐标原点O,且与x轴、y轴交于A、B两点,则△OAB的面积是( )
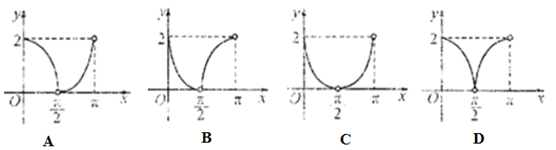
上,圆C过坐标原点O,且与x轴、y轴交于A、B两点,则△OAB的面积是( )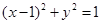 上异于坐标原点O的任意一点,直线OP的倾斜角为 ,若
上异于坐标原点O的任意一点,直线OP的倾斜角为 ,若 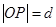 ,则函数
,则函数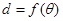 的大致图像是 ( )
的大致图像是 ( )