已知等比数列{an}的公比为q,记bn=am(n-1)+1+am(n-1)+2+…+am(n-1)+m,cn=am(n-1)+1·am(n-1)+2·…·am(n-1)+m(m,n∈N*),则以下结论一定正确的是( ).
| A.数列{bn}为等差数列,公差为qm |
| B.数列{bn}为等比数列,公比为q2m |
| C.数列{cn}为等比数列,公比为qm2 |
| D.数列{cn}为等比数列,公比为qmn |
在数列{an}中,a1=1,a2=2,且an+2-an=1+(-1)n(n∈N*),则S10=( ).
| A.2100 | B.2600 | C.2800 | D.3100 |
已知数列{an}满足:a1=1,an>0,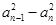 =1(n∈N*),那么使an<5成立的n的最大值为 ( ).
=1(n∈N*),那么使an<5成立的n的最大值为 ( ).
| A.4 | B.5 | C.24 | D.25 |
已知等差数列{an},若点(n,an)(n∈N*)在经过点(5,3)的定直线l1上,则数列{an}的前9项和S9=( ).
| A.9 | B.10 | C.18 | D.27 |
下面是关于公差d>0的等差数列{an}的四个命题:
p1:数列{an}是递增数列;
p2:数列{nan}是递增数列;
p3:数列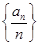 是递增数列;
是递增数列;
p4:数列{an+3nd}是递增数列.其中的真命题为( ).
| A.p1,p2 | B.p3,p4 | C.p2,p3 | D.p1,p4 |
已知等比数列{an}的公比为q,记bn=am(n-1)+1+am(n-1)+2+…+am(n-1)+m,cn=am(n-1)+1·am(n-1)+2·…·am(n-1)+m(m,n∈N*),则以下结论一定正确的是( )
| A.数列{bn}为等差数列,公差为qm |
| B.数列{bn}为等比数列,公比为q2m |
| C.数列{cn}为等比数列,公比为qm2 |
| D.数列{cn}为等比数列,公比为qmn |
在等差数列{an}中,a1+a5=10,a4=7,则数列{an}的公差为( )
| A.1 | B.2 | C.3 | D.4 |
若-9,a,-1成等差数列,-9,m,b,n,-1成等比数列,则ab=( ).
| A.15 | B.-15 | C.±15 | D.10 |
设{an}是公差不为0的等差数列,a1=2且a1,a3,a6成等比数列,则{an} 的前n项和Sn=( ).
A.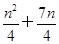 | B.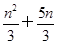 | C.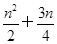 | D.n2+n |
在等差数列{an}中,a8= a11+6,则数列{an}前9项的和S9等于( ).
a11+6,则数列{an}前9项的和S9等于( ).
| A.24 | B.48 | C.72 | D.108 |