设函数f(x)=xex,则( )
| A.x=1为f(x)的极大值点 | B.x=1为f(x)的极小值点 |
| C.x=-1为f(x)的极大值点 | D.x=-1为f(x)的极小值点 |
已知函数f(x)=ax2+3x-2在点(2,f(2))处的切线斜率为7,则实数a的值为( )
| A.-1 | B.1 | C.±1 | D.-2 |
若S1=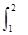 x2dx,S2=
x2dx,S2=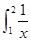 dx,S3=
dx,S3=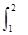 exdx,则S1,S2,S3的大小关系为( ).
exdx,则S1,S2,S3的大小关系为( ).
| A.S1<S2<S3 | B.S2<S1<S3 |
| C.S2<S3<S1 | D.S3<S2<S1 |
设函数f(x)在R上可导,其导函数为f′(x),且函数y=(2-x)f′(x)的图像如图所示,则下列结论中一定成立的是( )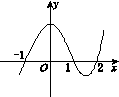
| A.函数f(x)有极大值f(1)和极小值f(-1) |
| B.函数f(x)有极大值f(1)和极小值f(2) |
| C.函数f(x)有极大值f(2)和极小值f(1) |
| D.函数f(x)有极大值f(-1)和极小值f(2) |
曲线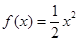 在点
在点 处的切线方程为( )
处的切线方程为( )
A.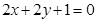 | B.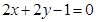 |
C.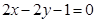 | D.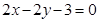 |
若函数
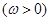 的图像在
的图像在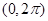 上恰有一个极大值和一个极小值,则
上恰有一个极大值和一个极小值,则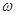 的取值范围是( )
的取值范围是( )
A.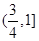 | B.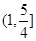 | C.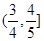 | D.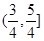 |
如图所示是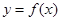 的导数
的导数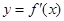 的图像,下列四个结论:
的图像,下列四个结论:
①  在区间
在区间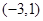 上是增函数;
上是增函数;
② 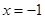 是
是 的极小值点;
的极小值点;
③  在区间
在区间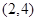 上是减函数,在区间
上是减函数,在区间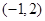 上是增函数;
上是增函数;
④ 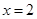 是
是 的极小值点.其中正确的结论是
的极小值点.其中正确的结论是
| A.①②③ |
| B.②③ |
| C.③④ |
| D.①③④ |
曲线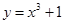 在点
在点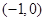 处的切线方程为
处的切线方程为
A.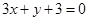 | B.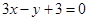 |
C.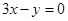 | D.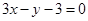 |
 的图象上的点
的图象上的点 处的切线的斜率为k,若
处的切线的斜率为k,若 ,则函数
,则函数