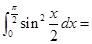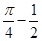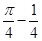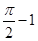已知甲、乙两车由同一起点同时出发, 并沿同一路线(假定为直线)行驶,甲车、乙车的速度曲线分别为v甲和v乙(如图所示).那么对于图中给定的t0和t1,下列判断中一定正确的是( )
| A.在t1时刻,甲车在乙车前面 |
| B.t1时刻后,甲车在乙车后面 |
| C.在t0时刻,两车的位置相同 |
| D.t0时刻后,乙车在甲车前面 |
已知定义在R上的可导函数f(x)的导函数为f′(x),满足f′(x)<f(x),且f(x+2)为偶函数,f(4)=1,则不等式f(x)<ex的解集为( )
| A.(-2,+∞) | B.(0,+∞) |
| C.(1,+∞) | D.(4,+∞) |
若0<x< ,则4x与3sin2x的大小关系是( )
,则4x与3sin2x的大小关系是( )
| A.4x>3sin2x | B.4x<3sin2x |
| C.4x=3sin2x | D.与x的取值有关 |
设f(x),g(x)在[a,b]上可导,且f′(x)>g′(x),则当a<x<b时,有( )
| A.f(x)>g(x) |
| B.f(x)<g(x) |
| C.f(x)+g(a)>g(x)+f(a) |
| D.f(x)+g(b)>g(x)+f(b) |
函数y=f(x)在定义域(-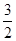 ,3)内的图像如图所示.记y=f(x)的导函数为y=f¢(x),则不等式f¢(x)≤0的解集为( )
,3)内的图像如图所示.记y=f(x)的导函数为y=f¢(x),则不等式f¢(x)≤0的解集为( )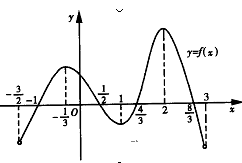
A.[-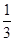 ,1]∪[2,3) ,1]∪[2,3) |
B.[-1, ]∪[ ]∪[ , , ] ] |
C.[-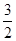 , , ]∪[1,2) ]∪[1,2) |
D.(-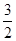 ,- ,-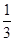 ]∪[ ]∪[ , , ]∪[ ]∪[ ,3) ,3) |
若实数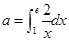 ,则函数
,则函数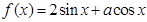 的图象的一条对称轴方程为( )
的图象的一条对称轴方程为( )
A.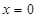 | B. | C.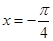 | D.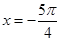 |
已知函数y=f(x)的图象关于y轴对称,且当x∈(-∞,0)时,f(x)+xf′(x)<0成立,a=(20.2)·f(20.2),b=(logπ3)·f(logπ3),c=(log39)·f(log39),则a,b,c的大小关系是( )
| A.b>a>c | B.c>a>b |
| C.c>b>a | D.a>c>b |
 的图像在点A(l,f(1))处的切线l与直线x十3y+2=0垂直,若数列
的图像在点A(l,f(1))处的切线l与直线x十3y+2=0垂直,若数列 的前n项和为
的前n项和为 ,则S2013的值为( )
,则S2013的值为( )



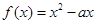 的图像在点A(l,f(1))处的切线l与直线x十3y+2=0垂直,若数列
的图像在点A(l,f(1))处的切线l与直线x十3y+2=0垂直,若数列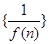 的前n项和为
的前n项和为 ,则S2013的值为 ( )
,则S2013的值为 ( )