已知曲线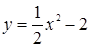 上一点P(1,
上一点P(1,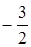 ),则过点P的切线的倾斜角为( )
),则过点P的切线的倾斜角为( )
| A.30° | B.45° | C.135° | D.165° |
对任意的x∈R,函数f(x)=x3+ax2+7ax不存在
极值点的充要条件是( )
| A.a=0或a="7" | B.a<0或a>21 | C.0≤a≤21 | D.a=0或a=21 |
已知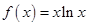 ,若
,若 则
则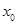 等于( )
等于( )
A.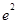 | B.e | C.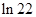 | D.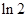 |
曲线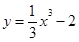 在点
在点 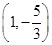 处切线的斜率为( )
处切线的斜率为( )
A. | B. | C. | D. |
函数f(x)的定义域是R,f(0)=2,对任意x∈R,f(x)+f′(x)>1,则不等式ex·f(x)>ex+1的解集为( )
| A.{x|x>0} |
| B.{x|x<0} |
| C.{x|x<-1或x>1} |
| D.{x|x<-1或0<x<1} |
设f(x)=- x3+
x3+ x2+2ax,若f(x)在(
x2+2ax,若f(x)在( ,+∞)上存在单调递增区间,则实数a的取值范围为( )
,+∞)上存在单调递增区间,则实数a的取值范围为( )
A.a>- | B.a<- | C.a> | D.不存在 |
若函数f(x)=2x2-lnx在其定义域内的一个子区间(k-1,k+1)内不是单调函数,则实数k的取值范围是( )
| A.[1,+∞) | B.[1,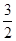 ) ) | C.[1,2) | D.[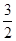 ,2) ,2) |
设函数f(x)在R上可导,其导函数为f′(x),且函数y=(1-x)f′(x)的图象如图所示,则下列结论中一定成立的是( )
| A.函数f(x)有极大值f(2)和极小值f(1) |
| B.函数f(x)有极大值f(-2)和极小值f(1) |
| C.函数f(x)有极大值f(2)和极小值f(-2) |
| D.函数f(x)有极大值f(-2)和极小值f(2) |
若a>0,b>0,且函数f(x)=4x3-ax2-2bx-2在x=1处有极值,则ab的最大值为( )
| A.2 | B.3 | C.6 | D.9 |
定义在R上的函数f(x)的导函数为f′(x),已知f(x+1)是偶函数,(x-1)f′(x)<0.若x1<x2,且x1+x2>2,则f(x1)与f(x2)的大小关系是( )
| A.f(x1)<f(x2) | B.f(x1)=f(x2) |
| C.f(x1)>f(x2) | D.不确定 |