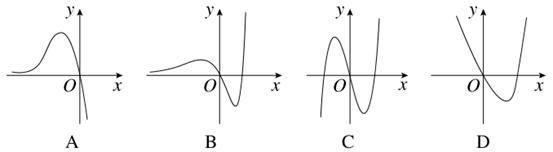
函数f(x)=x2-2ax+a在区间(-∞,1)上有最小值,则函数g(x)=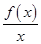 在区间(1,+∞)上一定( )
在区间(1,+∞)上一定( )
| A.有最小值 | B.有最大值 | C.是减函数 | D.是增函数 |
函数y=x4-4x+3在区间[-2,3]上的最小值为( )
| A.72 | B.36 | C.12 | D.0 |
函数f(x)=x2-2lnx的单调递减区间是( )
| A.(0,1] | B.[1,+∞) |
| C.(-∞,-1]∪(0,1] | D.[-1,0)∪(0,1] |
若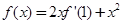 ,则
,则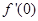 等于 ( )
等于 ( )
| A.-2 | B.-4 | C.2 | D.0 |
已知函数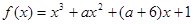 有极大值和极小值,则
有极大值和极小值,则 的取值范围为( )
的取值范围为( )
A.-1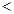  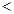 2 2 | B.-3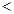  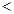 6 6 |
C. 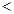 -1或 -1或 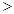 2 2 | D. 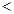 -3或 -3或 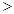 6 6 |
若函数 ,则
,则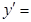 ( ).
( ).
A.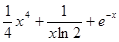 | B.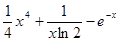 |
C.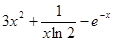 | D.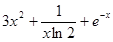 |
已知函数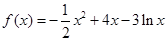 在
在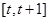 上不单调,则
上不单调,则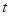 的取值范围是( )
的取值范围是( )
A. | B.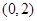 | C. | D. |
设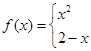
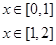 ,则
,则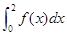 等于( )
等于( )
A.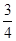 | B.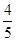 | C.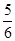 | D.不存在 |
设函数 在
在 上可导,则
上可导,则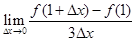 等于( )
等于( )
A.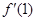 | B.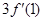 | C.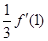 | D.以上都不对 |