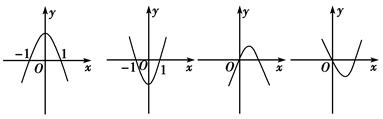
已知y=loga(2-ax)在[0,1]上是x的减函数,则a的取值范围是( )
| A.(0,1) | B.(1,2) |
| C.(0,2) | D.[2,+∞) |
已知函数f(x)=logax(a>0,a≠1)的图象,如下图所示,函数y=g(x)的图象与y=f(x)的图象关于直线y=x对称,则函数y=g(x)的解析式为( )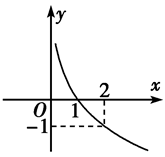
| A.g(x)=2x | B.g(x)=x |
| C.g(x)=logx | D.g(x)=log2x |
将函数y=+a的图象向右平移2个单位后又向下平移2个单位,所得图象的对称中心是(1,-1),那么a,b的值是( )
| A.a=-1,b≠0 | B.a=-1,b∈R |
| C.a=1,b≠0 | D.a=0,b∈R |
若函数f(x),g(x)分别是R上的奇函数、偶函数,且满足f(x)-g(x)=ex,则有( )
| A.f(2)<f(3)<g(0) | B.g(0)<f(3)<f(2) |
| C.f(2)<g(0)<f(3) | D.g(0)<f(2)<f(3) |
f(x),g(x)是定义在R上的函数,h(x)=f(x)+g(x),则“f(x),g(x)均为偶函数”是“h(x)为偶函数”的( )
| A.充要条件 |
| B.充分而不必要的条件 |
| C.必要而不充分的条件 |
| D.既不充分也不必要的条件 |
某电信公司推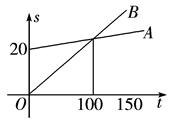 出两种手机收费方式:A种方式是月租20元,B种方式是月租0元.一个月的本地网内打出电话时间t(分钟)与打出电话费s(元)的函数关系如右图所示,当打出电话150分钟时,这两种方式电话费相差( )
出两种手机收费方式:A种方式是月租20元,B种方式是月租0元.一个月的本地网内打出电话时间t(分钟)与打出电话费s(元)的函数关系如右图所示,当打出电话150分钟时,这两种方式电话费相差( )
| A.10元 | B.20元 | C.30元 | D.元 |
某商场对顾客实行购物优惠活动,规定一次购物付款总额:①如果不超过200元,则不予优惠,②如果超过200元但不超过500元,则按标价给予9折优惠,③如果超过500元,其500元按②条给予优惠,超过500元的部分给予7折优惠.某人两次去购物,分别付款168元和423元,假设他一次购买上述同样的商品,则应付款( )
| A.413.7元 | B.513.7元 | C.546.6元 | D.548.7元 |