题目内容
某电信公司推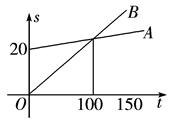 出两种手机收费方式:A种方式是月租20元,B种方式是月租0元.一个月的本地网内打出电话时间t(分钟)与打出电话费s(元)的函数关系如右图所示,当打出电话150分钟时,这两种方式电话费相差( )
出两种手机收费方式:A种方式是月租20元,B种方式是月租0元.一个月的本地网内打出电话时间t(分钟)与打出电话费s(元)的函数关系如右图所示,当打出电话150分钟时,这两种方式电话费相差( )
| A.10元 | B.20元 | C.30元 | D.元 |
A
解析

练习册系列答案
相关题目
函数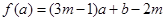 ,当
,当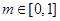 时,
时,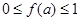 恒成立,则
恒成立,则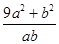
的最大值与最小值之和为 ( )
| A. 18 | B. 16 | C. 14 | D.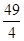 |
设函数
 ,若
,若 时,
时, >0恒成立,则实数m的取值范围是( )
>0恒成立,则实数m的取值范围是( )
| A.(0,1) | B.(-∞,0) | C.(-∞,) | D.(-∞,1) |
已知函数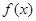 定义域为R,则
定义域为R,则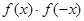 一定为 (
一定为 (
| A.偶函数 | B.奇函数 |
| C.非奇非偶函数 | D.既奇又偶函数 |
若x∈(e-1,1),a=ln x,b=2ln x,c=ln3x,则( )
| A.a<b<c | B.c<a<b |
| C.b<a<c | D.b<c<a |
已知函数f(x)=logax(a>0,a≠1)的图象,如下图所示,函数y=g(x)的图象与y=f(x)的图象关于直线y=x对称,则函数y=g(x)的解析式为( )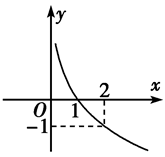
| A.g(x)=2x | B.g(x)=x |
| C.g(x)=logx | D.g(x)=log2x |
定义在R上的偶函数f(x)满足:对任意的x1,x2∈(-∞,0](x1≠x2),有(x2-x1)(f(x2)-f(x1))>0,则当n∈N*时,有
( )
| A.f(-n)<f(n-1)<f(n+1) |
| B.f(n-1)<f(-n)<f(n+1) |
| C.f(n+1)<f(-n)<f(n-1) |
| D.f(n+1)<f(n-1)<f(-n) |
设函数 ,则
,则
A. | B. | C. | D. |
、已知定义域为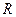 的函数
的函数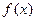 为偶函数,且当
为偶函数,且当 时,
时,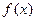 是减函数,设
是减函数,设
 ,
, ,则
,则 的大小关系是( )
的大小关系是( )
A. | B. | C. | D. |