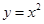的图象大致是
已知f（x）是以2为周期的偶函数，当x∈[0, 1]时，f（x）＝x，那么在区间[－1,3]内关于x的方程f（x）＝kx＋k＋1（k∈R，k≠－1）的根的个数
| A．不可能有3个 | B．最少有1个，最多有4个 |
| C．最少有1个，最多有3个 | D．最少有2个，最多有4个 |
已知
是定义在R上的奇函数，若对于x≥0，都有f(x+2)=，且
当
时，
，则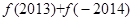
=（ ）
| A．1-e | B．e-1 | C．-l-e | D．e+l |
使得
的旋转性的是
已知函数
的定义域为
，且
为偶函数，则实数
的值可以是
A． | B． | C． | D． |
若函数
恰有三个不同的零点，则实数a的值是（ ）
| A．－1 | B． | C．1或 | D．－1或－ |
方程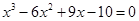
的实根个数是（ ）
| A．3 | B．2 | C．1 | D．0 |
若定义运算：
，例如
，则下列等式不能成立的是（ ）
A． | B． |
C． | D． （ ） |
设
是方程
的解，则属于区间 （ ）
| A．（0，1） | B．（1，2） | C．（2，3） | D．（3，4） |
函数
的定义域是 （ ）
A． | B． |
C． | D． |