已知函数f(x)= 为奇函数,则f(g(-1))=( )
为奇函数,则f(g(-1))=( )
| A.-20 | B.-18 | C.-15 | D.17 |
若不等式x2+ax+1≥0对于一切x∈(0, ]恒成立,则a的最小值是( )
]恒成立,则a的最小值是( )
| A.0 | B.2 | C.- | D.-3 |
函数f(x)=ax2+(a-3)x+1在区间[-1,+∞)上是递减的,则实数a的取值范围是( )
| A.[-3,0) | B.(-∞,-3] |
| C.[-2,0] | D.[-3,0] |
若f(x)=x2-x+a,f(-m)<0,则f(m+1)的值是( )
| A.正数 | B.负数 |
| C.非负数 | D.不能确定正负 |
已知函数y=x2-2x+3在闭区间[0,m]上有最大值3,最小值2,则m的取值范围是( )
| A.[1,+∞) | B.[0,2] |
| C.[1,2] | D.(-∞,2] |
函数f(x)= 的定义域为( )
的定义域为( )
| A.(0,+∞) | B.(1,+∞) |
| C.(0,1) | D.(0,1)∪(1,+∞) |
设f(x)是连续的偶函数,且当x>0时是单调函数,则满足f(2x)=f(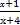 )的所有x之和为( )
)的所有x之和为( )
A.- | B.- | C.-8 | D.8 |
如图,虚线部分是四个象限的角平分线, 实线部分是函数y=f(x)的部分图象,则f(x)可能是( )
| A.x2sinx | B.xsinx |
| C.x2cosx | D.xcosx |
定义在R上的函数y=f(x+1)的图象如图所示,它在定义域上是减函数,给出如下命题:①f(0)=1;②f(-1)=1;③若x>0,则f(x)<0;④若x<0,则f(x)>0,其中正确的是( )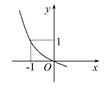
| A.②③ | B.①④ | C.②④ | D.①③ |
